Cho hình hộp \(ABCD.A'B'C'D'\) có thể tích bằng \(V\). Gọi \(M,\,\,N,\,\,P,\,\,Q,\,\,E,\,\,F\) lần lượt là tâm các hình bình hành \(ABCD,\,\,A'B'C'D',\,\,ABB'A',\,\,BCC'B',\,\,CDD'C',\,\,DAA'D'\). Thể tích khối đa diện có các đỉnh \(M,\,\,P,\,\,Q,\,\,E,\,\,F,\,\,N\) bằng:
Trả lời bởi giáo viên
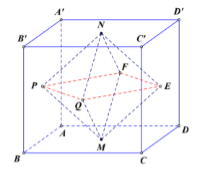
Đặc biệt hóa, coi \(ABCD.A'B'C'D'\) là khối lập phương cạnh bằng 1 \( \Rightarrow {V_{ABCD.A'B'C'D'}} = 1 = V\).
Dễ thấy \(MNPQEF\) là khối bát diện đều cạnh cạnh \(QE = \dfrac{1}{2}BD = \dfrac{{\sqrt 2 }}{2}\).
Vậy \({V_{MNPQEF}} = \dfrac{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^3}\sqrt 2 }}{3} = \dfrac{1}{6} = \dfrac{V}{6}\).
Hướng dẫn giải:
Đặc biệt hóa, coi \(ABCD.A'B'C'D'\) là khối lập phương cạnh bằng .
Sử dụng công thức tính nhanh thể tích khối bát diện đều cạnh \(a\) là \(V = \dfrac{{{a^3}\sqrt 2 }}{3}\).


