Cho hình chóp S.ABCD,O là điểm nằm bên trong tam giác ACD. Thiết diện của hình chóp cắt bởi mp(α) đi qua O và song song với AC và SD có số cạnh bằng:
Trả lời bởi giáo viên
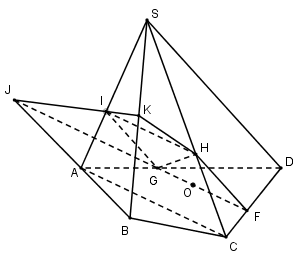
Trong (ABCD) qua O kẻ GF//AC(G∈AD,F∈CD)
Trong (SCD) qua F kẻ FH//SD(H∈SC)
⇒(α) là (GFH) .
(α)∩(ABCD)=GF,(α)∩(SCD)=HF.
Ta có: (α) và (SAC) có H chung, (α)⊃GF,(SAC)⊃AC,GF//AC.
⇒ Qua H kẻ HI//AC(I∈SA)
⇒(α)∩(SAC)=HI,(α)∩(SAD)=GI.
Trong (ABCD) gọi J=GF∩AB⇒J∈AB⇒J∈(SAB)
Trong (SAB) gọi K=IJ∩SB(K∈SB)
⇒(α)∩(SAB)=IK,(α)∩(SBC)=HK
Vậy thiết diện của hình chóp cắt bởi mp(α) là GFHKI là đa giác có 5 cạnh.
Hướng dẫn giải:
- Từ những giả thiết ban đầu xác định mp(α).
- Dựng thiết diện của mp(α) với hình chóp.
Giải thích thêm:
Khi xác định thiết diện của hình chóp cắt bởi mp(α) học sinh thường không xác định giao tuyến của mp(α) với tất cả các mặt của hình chóp dẫn đến thiết diện được xác định sai.

