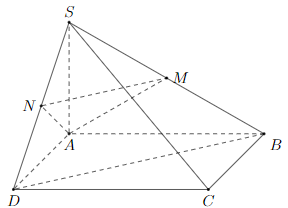
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA=a và vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung điểm của SB và SD. Biết sin góc giữa hai mặt phẳng (AMN) và (SBD) có dạng \(\dfrac{{a\sqrt b }}{9}\). Tính a+b.
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
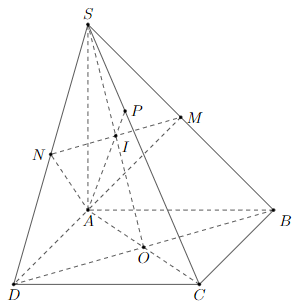
Gọi \(\alpha \) là góc giữa hai mặt phẳng (AMN) và (SBD)
O là trung điểm của BD
\(I\) là giao điểm của MN và SO và P là giao điểm của AI và SC
Ta có: \(\left\{ \begin{array}{l}SB \bot AM\\BC \bot AM\end{array} \right. \Rightarrow AM \bot \left( {SBC} \right)\)\( \Rightarrow AM \bot SC\)
Tương tự ta có: \(SC \bot \left( {AMN} \right)\)
Vì \(\left\{ \begin{array}{l}MN//BD\\BD \bot \left( {SOA} \right)\end{array} \right. \Rightarrow MN \bot \left( {SOA} \right)\)
Do vậy, \(\widehat {\left( {\left( {AMN} \right),\left( {SBD} \right)} \right)} = \widehat {\left( {AI,SO} \right)} = \widehat {PIS} = \alpha \)
Ta có:
\(\begin{array}{l}AO = \dfrac{{AB}}{{\sqrt 2 }} = a\sqrt 2 \\SO = \sqrt {A{O^2} + S{A^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \\SI = \dfrac{1}{2}SO = \dfrac{{a\sqrt 3 }}{2}\\SP = \dfrac{{S{A^2}}}{{SC}} = \dfrac{{{a^2}}}{{\sqrt {{a^2} + 2.4{a^2}} }} = \dfrac{a}{3}\end{array}\)
Vậy \(\sin \alpha = \dfrac{{SP}}{{SI}} = \dfrac{a}{3}.\dfrac{2}{{a\sqrt 3 }} = \dfrac{{2\sqrt 3 }}{9}\)
\(a + b = 2 + 3 = 5\)
Hướng dẫn giải:
Gọi \(\alpha \) là góc giữa hai mặt phẳng (AMN) và (SBD)
O là trung điểm của BD
\(I\) là giao điểm của MN và SO và P là giao điểm của AI và SC
Xác định góc giữa hai mặt phẳng (AMN) và (SBD)
Sử dụng hệ thức lượng trong tam giác vuông.
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 3 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
