Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(\widehat {BAD} = {60^0},\,\,SA = a\) và SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng \(\left( {SCD} \right)\) bằng:

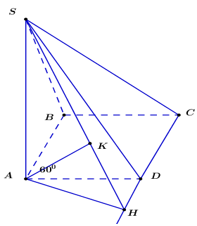
Ta có : \(AB//\left( {SCD} \right)\) \( \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right) = d\)

Kẻ \(AH \bot CD;\,\,AK \bot SH\)

\(\begin{array}{l}\left\{ \begin{array}{l}CD \bot SA\\CD \bot AH\end{array} \right. \Rightarrow CD \bot \left( {SAH} \right) \Rightarrow CD \bot AK \Rightarrow AK \bot \left( {SCD} \right)\\ \Rightarrow d\left( {B;\;\left( {SCD} \right)} \right) = d = AK.\end{array}\)

Xét \(\Delta AHD\) vuông tại \(H,\;\;\angle ADH = {60^0}\) ta có : \(AH = AD.\sin {60^0} = \dfrac{{a\sqrt 3 }}{2}\)

Áp dụng hệ thức lượng trong \(\Delta SAH\) vuông tại \(A\) có đường cao \(AK\) ta có :

\(AK = \dfrac{{SA.AH}}{{\sqrt {S{A^2} + A{H^2}} }} = \dfrac{{a.\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {{a^2} + \dfrac{{3{a^2}}}{4}} }} = \dfrac{{a\sqrt {21} }}{7} = d\)