Cho hình chóp S.ABCD có đáy là hình chữ nhật, biết AB=2a,AD=a,SA=3a và SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh CD. Khoảng cách giữa hai đường thẳng SC và BM bằng:
Trả lời bởi giáo viên
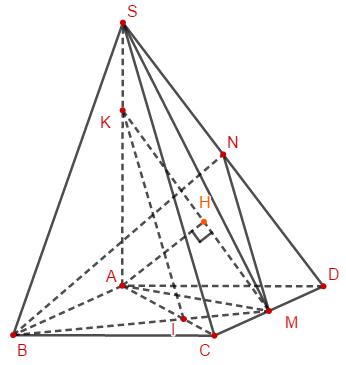
Gọi I là giao điểm của MB và AC, kẻ IK//SC(K∈SA), kẻ MN//SC(N∈SD). Khi đó KI,MN⊂(BMN). Kẻ AH⊥KM
Do ABCD là hình chữ nhật có AB=2CD nên AM⊥BM⇒BM⊥(SAM)
⇒(BMN)⊥(SAM)⇒AH⊥(BMN)
Ta có AI=2CI (vì CM//AB và AB=2CM)
Suy ra AK=2KS và
d(SC,BM)=d(SC,(BMN))=d(C,(BMN))=12d(A,(BMN))=12AH
AK=23SA=2a;AM=AD√2=a√2⇒1AH2=1AK2+1AM2=14a2+12a2=34a2⇒AH=2a√33
Hướng dẫn giải:
Dựng mặt phẳng (α) chứa BM và song song SC.
Khi đó d(BM,SC)=d(SC,(α))
Giải thích thêm:
Đối với lớp 12 có thể sử dụng phương pháp tọa độ như sau:
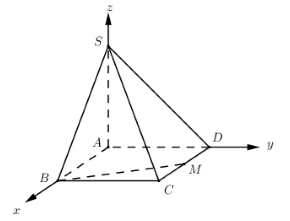
Đặt hệ trục toa độ như hình vẽ, chọn a=1. Khi đó ta có:
A(0;0;0),B(2;0;0),C(2;1;0);D(0;1;0);S(0;0;3)
M là trung điểm cạnh CD⇒M(1;1;0).
Ta có →SC=(−2;−1;3);→BM=(−1;1;0);→SB=(2;0;−3) ⇒[→SC;→BM]=(−3;−3;−3).
⇒d(SC;BM)=|[→SC;→BM].→SB||[→SC;→BM]|=|−3.2−3.0+(−3).(−3)|√(−3)2+(−3)2+(−3)2=33√3=√33


