Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = \dfrac{{a\sqrt 3 }}{2}\), tam giác \(ABC\) đều cạnh bằng \(a\) (minh họa như hình dưới). Góc tạo bởi giữa mặt phẳng\((SBC)\) và \(\left( {ABC} \right)\) bằng

Trả lời bởi giáo viên
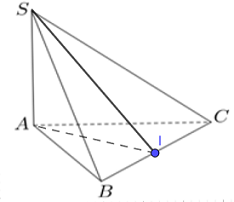
Gọi I là trung điểm của BC. Do tam giác ABC đều nên \(AI \bot BC\).
Mà \(SA \bot BC \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot SI\)
Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\AI \subset \left( {ABC} \right),\,\,AI \bot BC\\SI \subset \left( {SBC} \right),\,\,SI \bot BC\end{array} \right. \Rightarrow \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \left( {AI;SI} \right) = \widehat {SIA}\)
Tam giác \(ABC\) đều cạnh \(a\) \( \Rightarrow AI = \dfrac{{a\sqrt 3 }}{2}\)
Tam giác SAI vuông tại A \( \Rightarrow \tan \widehat {SIA} = \dfrac{{SA}}{{AI}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{{a\sqrt 3 }}{2}}} = 1 \Rightarrow \widehat {SIA} = {45^0}\)
Vậy \(\left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = {45^0}\).
Hướng dẫn giải:
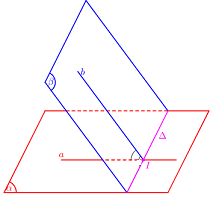
Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\):
- Tìm giao tuyến \(\Delta \) của \(\left( \alpha \right),\,\,\left( \beta \right)\).
- Xác định 1 mặt phẳng \(\left( \gamma \right) \bot \Delta \).
- Tìm các giao tuyến \(a = \left( \alpha \right) \cap \left( \gamma \right),b = \left( \beta \right) \cap \left( \gamma \right)\)
- Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\): \(\left( {\widehat {\left( \alpha \right);\left( \beta \right)}} \right) = \left( {\widehat {a;b}} \right)\)


