Câu hỏi:
2 năm trước
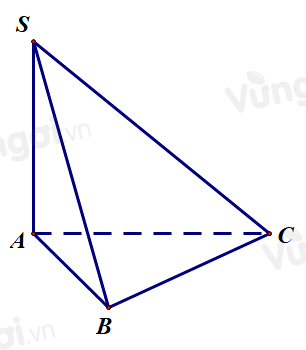
Cho hình chóp $S . A B C$ có đáy $A B C$ là tam giác đều cạnh a, cạnh bên $S A$ vuông góc với mặt phẳng đáy, góc giữa $S A$ và mặt phẳng \((SBC)\) bằng \({45^o}\) (tham khảo hình bên). Thể tích của khối chóp $S . A B C$ bằng
Trả lời bởi giáo viên
Đáp án đúng: a
Gọi \(M\) là trung điểm $B C$ thì \(AM \bot BC\) và \(SA \bot BC\) nên \(BC \bot (SAM)\).
Từ đây dễ thấy góc cân tìm là \(\alpha = \angle{ASM} = {45^o }\).
Do đó, SAM vuông cân ở \(A\) và \(SA = AM = \dfrac{{a\sqrt 3 }}{2}\).
Do tam giác $ABC$ là tam giác đều cạnh $a$ nên có diện tích là $S_{ABC}=\dfrac{a^2\sqrt{3}}{4}$
Suy ra \({V_{S.ABC}}= \dfrac{1}{3}SA.S_{ABC}\)\( = \dfrac{1}{3} \cdot \dfrac{{a\sqrt 3 }}{2} \cdot \dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}}}{8}\)
Hướng dẫn giải:
- Gọi \(M\) là trung điểm $B C$
- Chứng minh \(BC \bot (SAM)\)
- Diện tích của tam giác đều cạnh $a$ là $S=\dfrac{a^2\sqrt{3}}{4}$
- Tính thể tích của S.ABC.
