Câu hỏi:
3 năm trước
Cho hàm số \(y = f(x)\). Đồ thị hàm số \(y = {f^\prime }(x)\) như hình vẽ dưới đây:
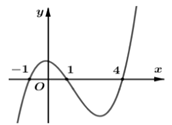
Số điểm cực trị của hàm số \(g(x) = {e^{2f(x) + 1}} + {5^{f(x)}}\) là
Trả lời bởi giáo viên
Đáp án đúng: c
Ta thấy đồ thị của hàm số \({f^\prime }(x)\) cắt trục hoành tại 3 điểm phân biệt, suy ra hàm số \(f(x)\) có 3 điểm cực trị.
Ta có \({g^\prime }(x) = 2{f^\prime }(x).{e^{2f(x) + 1}} + {f^\prime }(x){.5^{f(x)}}.\ln 5 = {f^\prime }(x).\left( {2{e^{2f(x) + 1}} + {5^{f(x)}}.\ln 5} \right)\).
Vì \(2{e^{2f(x) + 1}} + {5^{f(x)}}.\ln 5 > 0\) với mọi \(x\) nên \({g^\prime }(x) = 0 \Leftrightarrow {f^\prime }(x) = 0\).
Suy ra số điểm cực trị của hàm số \(g(x)\) bằng số điểm cực trị của hàm số \(f(x)\).
Hướng dẫn giải:
Chỉ ra số điểm cực trị của hàm số \(g(x)\) bằng số điểm cực trị của hàm số \(f(x)\).


