Cho hàm số \(y = f(x)\) có đạo hàm là \({f^\prime }(x) = {x^2} + 10x,\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = f\left( {{x^4} - 8{x^2} + m} \right)\) có đúng 9 điểm cực trị?

Ta có \({f^\prime }(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x =  - 10}\end{array}} \right.\)

\({y^\prime } = \left( {4{x^3} - 16x} \right) \cdot {f^\prime }\left( {{x^4} - 8{x^2} + m} \right) = 0\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{4{x^3} - 16x = 0}\\{{f^\prime }\left( {{x^4} - 8{x^2} + m} \right) = 0}\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2}\\{x =  - 2}\\{{x^4} - 8{x^2} + m = 0}\\{{x^4} - 8{x^2} + m =  - 10}\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2}\\{x =  - 2}\\{{x^4} - 8{x^2} =  - m(1)}\\{{x^4} - 8{x^2} =  - m - 10(2)}\end{array}} \right.\)

Để hàm số \(y = f\left( {{x^4} - 8{x^2} + m} \right)\) có 9 điểm cực trị thì \({f^\prime }\left( {{x^4} - 8{x^2} + m} \right) = 0\) phải có 6 nghiệm phân biệt.

Minh họa đồ thị hàm số $y={x^4} - 8{x^2}$ và các đường thẳng $y=-m$ và $y=-m-10$

Đường thẳng $y=-m$ nằm ở trên thì phải có 2 nghiệm và đường thẳng $y=-m-10$ ở dưới thì phải có 4 nghiệm.

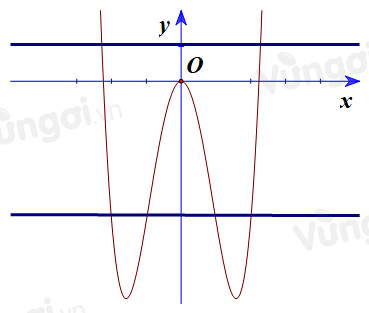
Suy ra phương trình (1) phải có 2 nghiệm và phương trình (2) phải có 4 nghiệm

Ta có : \(\left\{ {\begin{array}{*{20}{l}}{ - m \ge 0}\\{ - 16 <  - m - 10 < 0}\end{array}} \right.\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \le 0}\\{ - 10 < m < 6}\end{array} \Leftrightarrow  - 10 < m \le 0} \right.\).

Do \(m \in \mathbb{Z}\) nên \(m \in \{  - 9; - 8; \ldots ; - 1;0\} \).

Vậy có 10 giá trị nguyên m.