Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:

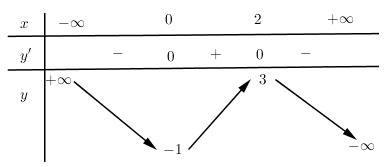
Bảng biến thiên trên là bảng biến thiên của hàm số nào?

Nhận xét: Dễ thấy bảng biến thiên của đồ thị hàm số bậc 3 nên loại đáp án B.

Ngoài cùng bên phải của $y< 0 \Rightarrow a < 0$ nên loại đáp án A.

Thay lần lượt hai điểm $\left( {0;\, - 1} \right)$ và $\left( {2;\,3} \right)$ vào 2 hàm số còn lại.

Thay $x = 0$ vào cả hai  hàm số $y =  - {x^3} + 3{x^2} - 1$ và $y =  - {x^3} - 3{x^2} - 1$ ta thu được $y =  - 1$ $ \Rightarrow \left( {0;\, - 1} \right)$ đều thuộc vào 2 đồ thị hàm số $y =  - {x^3} + 3{x^2} - 1$ và $y =  - {x^3} - 3{x^2} - 1$

Thay $x = 2$ vào hàm số $y =  - {x^3} + 3{x^2} - 1$ ta được $ y = 3 \Rightarrow \left( {2;\,3} \right)$ thuộc vào đồ thị hàm số $y =  - {x^3} + 3{x^2} - 1$.

Thay $x = 2$ vào hàm số $y =  - {x^3} - 3{x^2} - 1$ ta được $y =  - 21$ $ \Rightarrow \left( {2;\,3} \right)$ không thuộc vào đồ thị hàm số $y =  - {x^3} - 3{x^2} - 1$.