Câu hỏi:
2 năm trước
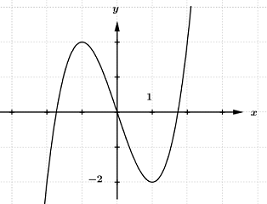
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có bốn nghiệm phân biệt.
Trả lời bởi giáo viên
Đáp án đúng: c
Dựa vào đồ thị hàm số \(y = f\left( x \right)\) ta suy ra được đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) như sau:
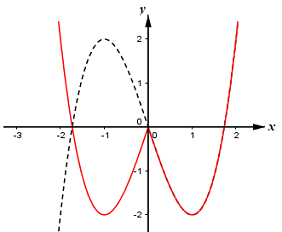
Số nghiệm của phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = 3m + 1\) song song với trục hoành.
Do đó để phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có 4 nghiệm phân biệt thì \( - 2 < 3m + 1 < 0 \Leftrightarrow - 1 < m < - \dfrac{1}{3}\).
Hướng dẫn giải:
- Vẽ đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\).
+ Vẽ đồ thị hàm số \(y = f\left( x \right)\).
+ Xóa đi phần đồ thị hàm số nằm ở bên trái trục tung.
+ Lấy đối xứng phần đồ thị hàm số nằm ở bên phải trục tung qua trục tung.
- Biện luận nghiệm để tìm tham số m: Số nghiệm của phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = 3m + 1\) song song với trục hoành.
Câu hỏi khác
- Đề thi kiểm tra 15 phút chương 1: Hàm số - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 1: Hàm số - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 1: Hàm số - Đề số 3 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 1: Hàm số - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 1: Hàm số - Đề số 3 Toán 12 có lời giải chi tiết
