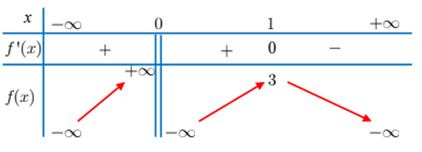
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên:
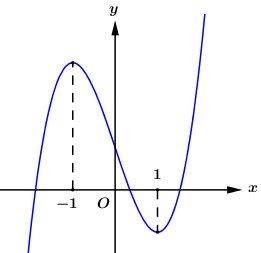
Giá trị nguyên lớn nhất của tham số m để hàm số \(y = f\left( {\left| x \right| - m} \right)\) đồng biến trên khoảng \(\left( {10; + \infty } \right)\) là:
Trả lời bởi giáo viên
Ta có \(y = f\left( {\left| x \right| - m} \right) = f\left( {\sqrt {{x^2}} - m} \right)\).
\( \Rightarrow y' = \dfrac{{2x}}{{2\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right) = \dfrac{x}{{\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right)\).
Để hàm số đồng biến trên \(\left( {10; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\).
\( \Rightarrow \dfrac{x}{{\sqrt {x^2} }}f'\left( {\sqrt {x^2} - m } \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow f'\left( {\sqrt {x^2} - m} \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\,\,\left( * \right)\).
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên \(\left( {1; + \infty } \right)\) và \(\left( { - \infty ; - 1} \right)\).
Do đó \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}\sqrt {{x^2}} - m \ge 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\,\,\,\left( 1 \right)\\\sqrt {{x^2}} - m \le - 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\left( 2 \right)\end{array} \right.\)
Xét (1) ta có \(m \le \sqrt {{x^2}} - 1\,\,\forall x \in \left( {10; + \infty } \right) \Rightarrow m \le \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right)\).
Xét \(g\left( x \right) = \sqrt {{x^2}} - 1\) trên khoảng \(\left( {10; + \infty } \right)\) ta có \(g'\left( x \right) = \dfrac{x}{{\sqrt {{x^2}} }} > 0\,\,\forall x \in \left( {10; + \infty } \right)\), do đó hàm số đồng biến trên \(\left( {10; + \infty } \right)\) \( \Rightarrow \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right) = g\left( {10} \right) = 9 \Leftrightarrow m \le 9\).
Xét (2) ta có: \(m \ge \sqrt {{x^2}} + 1\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow m \ge \mathop {\max }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} + 1} \right)\).
Do \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2}} + 1} \right) = + \infty \) nên hàm số đã cho không có GTLN trên \(\left[ {10; + \infty } \right)\), do đó không tồn tại m thỏa mãn (2).
Vậy \(m \le 9\) nên giá trị nguyên lớn nhất của m bằng 9.
Hướng dẫn giải:
- Biến đổi \(f\left( {\left| x \right| - m} \right) = f\left( {\sqrt {{x^2}} - m} \right)\).
- Tính đạo hàm của hàm số.
- Để hàm số đồng biến trên \(\left( {10; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\).
- Dựa vào BBT xác định các khoảng đồng biến của hàm số.
- Sử dụng phương pháp cô lập m.
Giải thích thêm:
Cách 2:
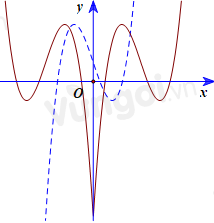
Ta vẽ đồ thị của hàm số \(y = f\left( {\left| x \right| - m} \right)\) với m>0
Tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang phải m đơn vị, sau đó bỏ phần đồ thị của \(f\left( {x - m} \right)\) phía bên trái Oy. Lấy đối xứng phần đồ thị hàm số \(f\left( {x - m} \right)\) phía bên phải Oy qua Oy
Khi đó hàm số $f(x)$ đồng biến trên $\left( {1 ; + \infty } \right)$
=> Hàm số $y=f(x-m)$ đồng biến trên $\left( {1 +m; + \infty } \right)$
=> Hàm số $y=f(|x|-m)$ đồng biến trên $\left( {1 +m; + \infty } \right)$
Để hàm số \(y = f\left( {\left| x \right| - m} \right)\) đồng biến trên khoảng \(\left( {10; + \infty } \right)\) thì ta chỉ cần xét khoảng đồng biến của hàm số \(y = f\left( {\left| x \right| - m} \right)\) trên $\left( {1 +m; + \infty } \right)$ là được.
\(\left( {10; + \infty } \right) \subset \left( {1 + m; + \infty } \right) \Rightarrow 1 + m \le 10\)\( \Leftrightarrow m \le 9\).
Vậy giá trị nguyên lớn nhất của m là 9