Câu hỏi:
2 năm trước
Cho hàm số $y = \dfrac{{2mx + m}}{{x - 1}}\left( C \right).$. Với giá trị nào của $m \left({m\ne0}\right)$ thì đường tiệm cận đứng, đường tiệm cận ngang của đồ thị hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng $8$?
Trả lời bởi giáo viên
Đáp án đúng: c
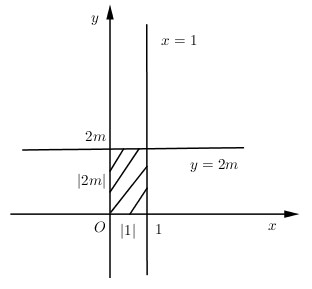
$y=\dfrac{2mx+m}{x-1}\left| \begin{align}& \xrightarrow{TCD}x=1 \\ & \xrightarrow{TCN}y=2m \\ \end{align}\right.$
$S = 8 \Leftrightarrow \left| {2m} \right|.\left| 1 \right| = 8 \Leftrightarrow \left| {2m} \right| = 8 \Leftrightarrow 2m = \pm 8 \Leftrightarrow m = \pm 4$
Hướng dẫn giải:
- Tìm các tiệm cận đứng và ngang của đồ thị hàm số.
- Sử dụng công thức diện tích hình chữ nhật $S = ab$ để tìm $m$.