Cho hàm số $y = \dfrac{{2{x^2} - 3{x} + m}}{{x - m}}$ . Để đồ thị hàm số không có tiệm cận đứng thì các giá trị của tham số $m$ là:
Trả lời bởi giáo viên
Cách 1: Thử đáp án
Với $m = 0$ ta có $x = 0$ là nghiệm của đa thức $2{x^2} - 3{\text{x}}$ trên tử
$ \Rightarrow y = 2{\text{x}} - 3\left( {x \ne 0} \right)$ không có tiệm cận đứng.
Với $m = 1$ ta có $x = 1$ là nghiệm của đa thức $2{x^2} - 3{\text{x + 1}}$ trên tử
$ \Rightarrow y = 2{\text{x}} - 1\left( {x \ne 1} \right)$ không có tiệm cận đứng.
Cách 2: Chia đa thức
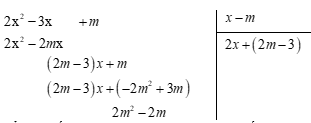
Để hàm số không có tiệm cận đứng thì tử số phải chia hết cho mẫu số
$ \Leftrightarrow 2{m^2} - 2m = 0 \Leftrightarrow m = 0$ hoặc $m = 1$
Hướng dẫn giải:
Đồ thị hàm số $y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}$ không có tiệm cận đứng nếu mọi nghiệm của $g\left( x \right)$ (nếu có) đều là nghiệm của $f\left( x \right)$.