Câu hỏi:
2 năm trước
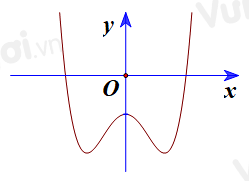
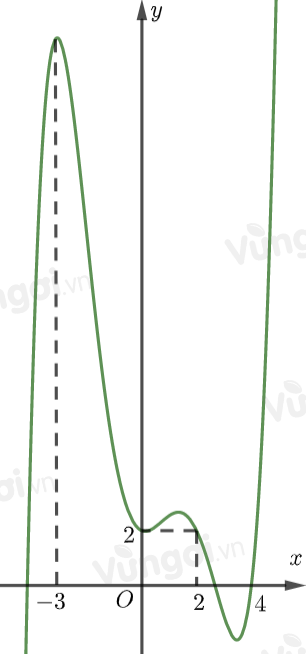
Cho hàm số \(f(x)\), đồ thị của hàm số \(y = {f^\prime }(x)\) là đường cong trong hình bên. Giá trị lớn nhất của hàm số \(g(x) = f(2x) - 4x\) trên đoạn \(\left[ { - \dfrac{3}{2};2} \right]\) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
Đặt \(2x = t\) thì \(t \in [ - 3;4]\) và ta đưa về xét \(g\left( x \right) = h(t) = f(t) - 2t\). Ta có \({h^\prime }(t) = {f^\prime }(t) - 2\) nên dựa vào đồ thị đã cho thì \({h^\prime }(t) = 0\) có hai nghiệm \(t = 0,t = 2\), trong đó \({f^\prime }(t) - 2\) lại không đổi dấu khi qua \(t = 0\), còn \({h^\prime }(t)\) đổi dấu từ $+$ sang $-$ khi qua \(t = 2\).
Lập bảng biến thiên cho \(h(t)\) trên \([ - 3;4]\)
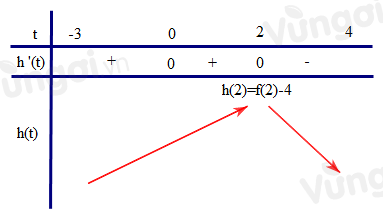
=> max \(h(t) = h(2) = f(2) - 4\).
Hướng dẫn giải:
- Đặt \(2x = t\), ta đưa về xét \(h(t) = f(t) - 2t\).
- Tìm nghiệm của \({h^\prime }(t) = 0\)
- Lập bảng biến thiên và tìm max\(g(x) = f(2x) - 4x\)
