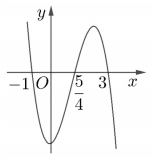
Cho hàm số \(f\left( x \right) = m{x^4} + n{x^3} + p{x^2} + qx + r\) \(\left( {m,n,p,q,r \in R} \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Tập nghiệm của phương trình \(f\left( x \right) = r\) có số phần tử là

\(f\left( x \right) = m{x^4} + n{x^3} + p{x^2} + qx + r\)

Từ đồ thị hàm số \(y = f'\left( x \right)\) dễ thấy \(m \ne 0\).

Phương trình \(f\left( x \right) = r \Leftrightarrow m{x^4} + n{x^3} + p{x^2} + qx = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\m{x^3} + n{x^2} + px + q = 0\,\,\left( * \right)\end{array} \right.\)

Xét \(f'\left( x \right) = 4m{x^3} + 3n{x^2} + 2px + q = 0\) có ba nghiệm \({x_1} =  - 1;{x_2} = \dfrac{5}{4};{x_3} = 3\).

Theo hệ thức Vi-et : \(\left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} =  - \dfrac{b}{a}\\{x_1}{x_2} + {x_2}{x_3} + {x_3}{x_1} = \dfrac{c}{a}\\{x_1}{x_2}{x_3} =  - \dfrac{d}{a}\end{array} \right.\) ta có: \(\left\{ \begin{array}{l}\dfrac{{13}}{4} =  - \dfrac{{3n}}{{4m}}\\ - \dfrac{1}{2} = \dfrac{{2p}}{{4m}}\\ - \dfrac{{15}}{4} =  - \dfrac{q}{{4m}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}n =  - \dfrac{{13}}{3}m\\p =  - m\\q = 15m\end{array} \right.\)

Thay vào \(\left( * \right)\) được \(m{x^3} - \dfrac{{13}}{3}m{x^2} - mx + 15m = 0 \Leftrightarrow {x^3} - \dfrac{{13}}{3}{x^2} - x + 15 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{5}{3}\\x = 3\end{array} \right.\)

Vậy phương trình đã cho có \(3\) nghiệm phân biệt \({x_1} = 0;\;{x_2} = 3;\;{x_3} =  - \dfrac{5}{3}\)