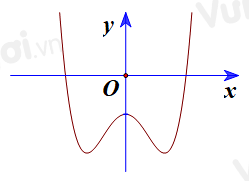
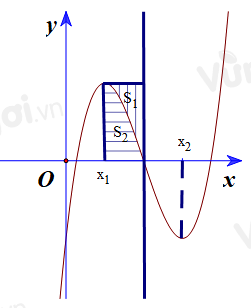
Cho hàm số bậc ba \(y = f(x)\) có đồ thị là đường cong trong hình bên. Biết hàm số \(f(x)\) đạt cực trị tại hai điểm \({x_1},{x_2}\) thỏa mãn \({x_2} = {x_1} + 2\) và \(f\left( {{x_1}} \right) + f\left( {{x_2}} \right) = 0\). Gọi \({S_1}\) và \({S_2}\) là diện tích của hai hình phẳng được gạch trong hình bên. Tỉ số \(\dfrac{{{S_1}}}{{{S_2}}}\) bằng

Kết quả bài toán không đổi nếu ta tịnh tiến đồ thị sang trái cho điểm uốn trùng gốc tọa độ \(O\).

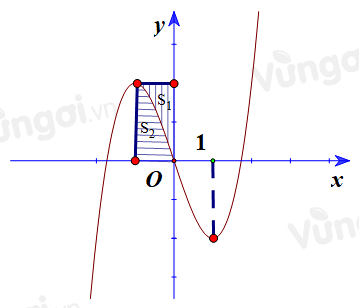
Gọi \(g(x) = a{x^3} + b{x^2} + cx + d\) là hàm số khi đó thì dễ thấy \(g(x)\) lẻ nên có ngay \(b = d = 0\) và \(g(x) = a{x^3} + cx\) có hai điểm cực trị tương ứng là \( - 1,1\), cũng là nghiệm của \(3a{x^2} + c = 0\). Từ đó dễ dàng có \(g(x) = k\left( {{x^3} - 3x} \right)\) với \(k > 0\).

Xét diện tích hình chữ nhật \({S_1} + {S_2} = |( - 1) \cdot g( - 1)| = 2k\). Ngoài ra,

\({S_2} = k\int_{ - 1}^0 {\left| {{x^3} - 3x} \right|} {\rm{d}}x = \dfrac{5}{4}k\)

Vì thế \({S_1} = 2k - \dfrac{{5k}}{4} = \dfrac{{3k}}{4}\) và \(\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{3}{5}\).