Câu hỏi:
2 năm trước
Cho hai đường thẳng $x$ và $y$ cắt nhau tại $O$ (như hình vẽ).
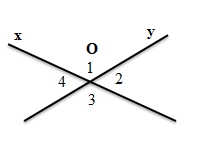
Biết \(\widehat {{O_2}} + \widehat {{O_4}} = {100^0}\). Tính \(\widehat {{O_3}}\)
Trả lời bởi giáo viên
Đáp án đúng: d

Ta có: \(\widehat {{O_2}} = \widehat {{O_4}}\) (đối đỉnh), mà $\widehat {{O_2}} + \widehat {{O_4}} = {100^0}\left( {gt} \right) \Rightarrow \widehat {{O_2}}\, = \widehat {{O_4}} = {100^0}:2 = {50^0}$
Lại có:\(\widehat {{O_2}} + \widehat {{O_3}} = {180^0}\) (kề bù) \( \Rightarrow \widehat {{O_3}} = {180^0} - {50^0} = {130^0}\)
Hướng dẫn giải:
Áp dụng tính chất: hai góc đối đỉnh thì bằng nhau.
Áp dụng hai góc kề bù có tổng số đo bằng \(180^\circ \)