Cho hai đoạn thẳng $AB$ và $CD$ cắt nhau ở $E.$ Các tia phân giác của các góc $ACE$ và $DBE$ cắt nhau ở $K.$ Chọn câu đúng.
Trả lời bởi giáo viên
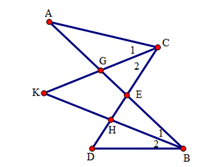
Gọi \(G = CK \cap AE;\,H = BK \cap DE\) .
Xét tam giác $KGB$ có: \(\widehat K + \widehat {{B_1}} = 180^\circ - \widehat {KGB}\) ( định lí tổng ba góc trong tam giác)
Xét tam giác $KGB$ có: \(\widehat A + \widehat {{C_1}} = 180^\circ - \widehat {AGC}\) ( định lí tổng ba góc trong tam giác)
Mà \(\widehat {KGB} = \widehat {AGC}\) (hai góc đối đỉnh), suy ra \(\widehat K + \widehat {{B_1}} = \widehat A + \widehat {{C_1}}\) (1)
Xét tam giác KHC có: \(\widehat K + \widehat {{C_2}} = 180^\circ - \widehat {KHC}\)( định lí tổng ba góc trong tam giác)
Xét tam giác DHB có: \(\widehat D + \widehat {{B_2}} = 180^\circ - \widehat {DHB}\)( định lí tổng ba góc trong tam giác)
Mà \(\widehat {KHC} = \widehat {DHB}\) (hai góc đối đỉnh), suy ra \(\widehat K + \widehat {{C_2}} = \widehat D + \widehat {{B_2}}\) (2)
Cộng vế với vế của biểu thức (1) và (2) ta được: \(2\widehat K + \widehat {{B_1}} + \widehat {{C_2}} = \widehat A + \widehat D + \widehat {{B_2}}+ \widehat {{C_1}}.\)
MÀ \(\widehat {{B_1}} = \widehat {{B_2}}\) (BK là tia phân giác của góc DBA);
\(\widehat {{C_1}} = \widehat {{C_2}}\) ( CK là tia phân giác của góc ACD).
\( \Rightarrow 2\widehat K = \widehat A + \widehat D\), do đó \(\widehat K = \dfrac{{\widehat A + \widehat D}}{2}\) hay \(\widehat {BKC} = \dfrac{{\widehat {BAC} + \widehat {BDC}}}{2}\).
Hướng dẫn giải:
+ Gọi \(G = CK \cap AE;\,H = BK \cap DE\)
+ Dựa vào tính chất tổng các góc của một tam giác, hai góc đối đỉnh
+ Sử dụng tính chất tia phân giác.