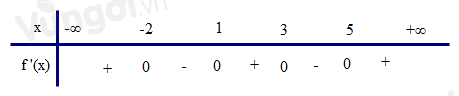Cho \(f(x)\) là hàm số bậc bốn thỏa mãn \(f(0) = 0\). Hàm số \({f^\prime }(x)\) có bảng biến thiên như sau:

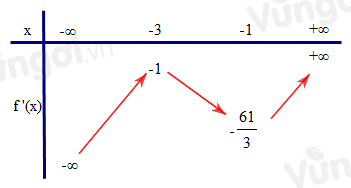
Hàm số \(g(x) = \left| {f\left( {{x^3}} \right) - 3x} \right|\) có bao nhiêu điểm cực trị?

Ta có \({f^\prime }(x)\) bậc ba có 2 điểm cực trị là \(x =  - 3,x =  - 1\) nên \({f^{\prime \prime }}(x) = a(x + 3)(x + 1)\).

Suy ra \({f^\prime }(x) = a\left( {\dfrac{{{x^3}}}{3} + 2{x^2} + 3x} \right) + b.\)

Do \(f'( - 3) =  - 1\) và \(f'( - 1) =  - \dfrac{{61}}{3}\)

=>\(a = \dfrac{{29}}{2},b =  - 1\) hay \({f^\prime }(x) = \dfrac{{29}}{2}\left( {\dfrac{{{x^3}}}{3} + 2{x^2} + 3x} \right) - 1\).

Do đó \({f^\prime }(0) =  - 1 < 0\).

Đặt \(h(x) = f\left( {{x^3}} \right) - 3x\) thì \({h^\prime }(x) = 3{x^2}{f^\prime }\left( {{x^3}} \right) - 3\) nên \({h^\prime }(x) = 0 \Leftrightarrow {f^\prime }\left( {{x^3}} \right) = \dfrac{1}{{{x^2}}}\).(*)

Với $x<0$ thì \({f^\prime }(x) < 0\) nên \({f^\prime }\left( {{x^3}} \right) < 0,\forall x < 0\)

=> (*) vô nghiệm trên \(( - \infty ;0]\) (Do $x\ne 0$)

Xét \(x > 0\) thì \({f^\prime }(x)\) đồng biến còn \(\dfrac{1}{{{x^2}}}\) nghịch biến nên (*) có không quá 1 nghiệm.

Lại có \(\mathop {\lim }\limits_{x \to {0^ + }} \left( {{f^\prime }\left( {{x^3}} \right) - \dfrac{1}{{{x^2}}}} \right) =  - \infty \) và \(\mathop {\lim }\limits_{x \to  + \infty } \left( {{f^\prime }\left( {{x^3}} \right) - \dfrac{1}{{{x^2}}}} \right) =  + \infty \) nên (*) có đúng nghiệm \(x = c > 0\).

Xét bảng biến thiên của \(h(x)\) :

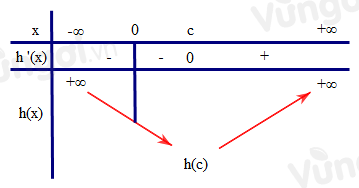
Vì \(h(0) = f(0) = 0\) nên \(h(c) < 0\) và phương trình \(h(x) = 0\) có hai nghiệm thực phân biệt, khác \(c\).

Từ đó \(|h(x)|\) sẽ có 3 điểm cực trị.