Cho $f\left( x \right)$ mà đồ thị hàm số $y = f'\left( x \right)$ như hình vẽ bên

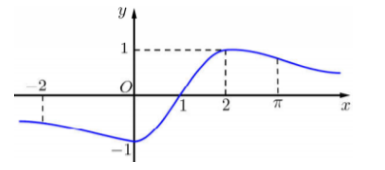
Bất phương trình $f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m$ nghiệm đúng với mọi $x \in \left[ { - 1;3} \right]$ khi và chỉ khi:

$\begin{array}{l}f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\,\,\forall x \in \left[ { - 1;3} \right] \Leftrightarrow g\left( x \right) = f\left( x \right) - \sin \dfrac{{\pi x}}{2} > m\,\,\forall x \in \left[ { - 1;3} \right]\\ \Rightarrow m < \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\end{array}$.

Từ đồ thị hàm số $y = f'\left( x \right)$ ta suy ra BBT đồ thị hàm số $y = f\left( x \right)$ như sau:

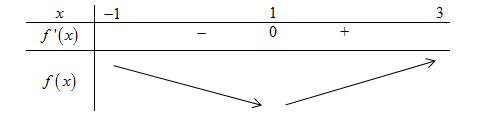
Dựa vào BBT ta thấy $f\left( x \right) \ge f\left( 1 \right)\,\,\forall x \in \left[ { - 1;3} \right]$.

$\begin{array}{l}x \in \left[ { - 1;3} \right] \Rightarrow \dfrac{{\pi x}}{2} \in \left[ { - \dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right] \Rightarrow  - 1 \le \sin \dfrac{{\pi x}}{2} \le 1\\ \Leftrightarrow  - 1 \le  - \sin \dfrac{{\pi x}}{2} \le 1\end{array}$

$\Rightarrow f\left( 1 \right) - 1 \le f\left( x \right) - \sin \dfrac{{\pi x}}{2} \Leftrightarrow g\left( x \right) \ge f\left( 1 \right) - 1 \Rightarrow \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right) = f\left( 1 \right) - 1$.

Vậy $m < f\left( 1 \right) - 1$.