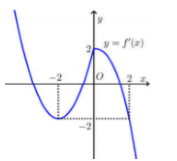
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Hàm số \(y = f\left( {x - 1} \right) + {x^2} - 2x\) đồng biến trên khoảng?

Ta có: \(y' = f'\left( {x - 1} \right) + 2x - 2 = 0\) \( \Leftrightarrow f'\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\).

Đặt \(t = x - 1\) ta có \(f'\left( t \right) + 2t = 0\) \( \Leftrightarrow f'\left( t \right) - \left( { - 2t} \right) = 0\).

Vẽ đồ thị hàm số \(y = f'\left( t \right)\) và \(y =  - 2t\) trên cùng mặt phẳng tọa độ ta có:

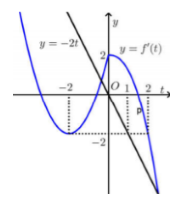
Xét \(y' \ge 0 \Leftrightarrow f'\left( t \right) \ge  - 2t \Rightarrow \) Đồ thị hàm số \(y = f'\left( t \right)\) nằm trên đường thẳng \(y =  - 2t\).

Xét \(x \in \left( {1;2} \right) \Rightarrow t \in \left( {0;1} \right) \Rightarrow \) thỏa mãn.

Xét \(x \in \left( { - 1;0} \right) \Rightarrow t \in \left( { - 2; - 1} \right) \Rightarrow \) Không thỏa mãn.

Xét \(x \in \left( {0;1} \right) \Rightarrow t \in \left( { - 1;0} \right) \Rightarrow \) Không thỏa mãn.

Xét \(x \in \left( { - 2; - 1} \right) \Rightarrow t \in \left( { - 3; - 2} \right) \Rightarrow \) Không thỏa mãn.