Câu hỏi:
3 năm trước
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(A{B^2}\) bằng
Trả lời bởi giáo viên
Đáp án đúng: a
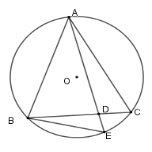
Xét \(\left( O \right)\) có \(\widehat {AEB} = \widehat {ABC}\) (hai góc nội tiếp chắn hai cung bằng nhau \(AB = AC\) )
Xét \(\Delta ABD\) và \(\Delta AEB\) có \(\widehat A\) chung và \(\widehat {AEB} = \widehat {ABC}\) (cmt) nên \(\Delta ABD\backsim\Delta AEB\left( {g - g} \right) \Rightarrow \dfrac{{AB}}{{AE}} = \dfrac{{AD}}{{AB}} \Rightarrow A{B^2} = AE.AD\)
Hướng dẫn giải:
Sử dụng hệ quả của góc nội tiếp để chứng minh các góc bằng nhau và suy ra tam giác đồng dạng
Từ đó có hệ thức cần chứng minh.


