Câu hỏi:
2 năm trước
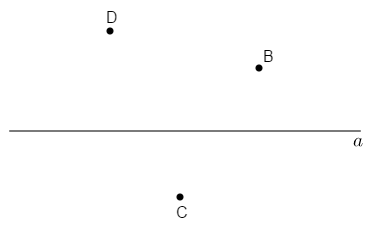
Cho đường thẳng \(a\) và bốn điểm \(M;N;P;Q\) trong đó \(M;N\) thuộc cùng nửa mặt phẳng có bờ \(a\) và \(P;Q\) cùng thuộc nửa mặt phẳng còn lại có bờ \(a.\) Khi đó đường thẳng \(a\) cắt bao nhiêu đoạn thẳng?
Trả lời bởi giáo viên
Đáp án đúng: d
Vì \(M;N\) nằm khác phía với \(P;Q\) nên ta có
+) \(P\) và \(M\) nằm khác phía so với đường thẳng \(a\) suy ra đường thẳng \(a\) cắt đoạn \(PM.\)
+) \(P\) và \(N\) nằm khác phía so với đường thẳng \(a\) suy ra đường thẳng \(a\) cắt đoạn \(PN.\)
+) \(Q\) và \(M\) nằm khác phía so với đường thẳng \(a\) suy ra đường thẳng \(a\) cắt đoạn \(QM.\)
+) \(Q\) và \(N\) nằm khác phía so với đường thẳng \(a\) suy ra đường thẳng \(a\) cắt đoạn \(QN.\)
Vậy đường thẳng \(a\) cắt bốn đoạn thẳng \(PM;PN;QM;QN.\)
Hướng dẫn giải:
+ Xác định các cặp điểm thuộc hai nửa mặt phẳng đối nhau bờ \(a.\)
+ Đoạn thẳng tạo thành từ mỗi cặp điểm đó là đoạn thẳng cắt đường thẳng \(a.\)
