Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {120^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), lấy \(D\) sao cho \(BCD\) là tam giác đều. Khi đó
Trả lời bởi giáo viên
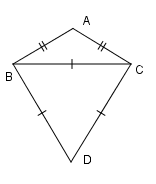
Ta có $\Delta BCD$ là tam giác đều nên \(\widehat {DCB} = {60^0}\,\,\left( 1 \right).\) Mặt khác \(\Delta ABC\) là tam giác cân tại \(A\) có $\widehat {BAC} = {120^0}$ hơn nữa tổng ba góc trong một tam giác bằng \({180^0}\) nên ta nhận được
\(\left\{ \begin{array}{l}\widehat {ACB} = \widehat {ABC}\\\widehat {ACB} + \widehat {ABC} + \widehat {BAC} = {180^0}\end{array} \right. \Rightarrow \widehat {ACB} = {30^0}\,\,\,\,\left( 2 \right)\) .
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có \(\widehat {DCA} = \widehat {DCB} + \widehat {BCA} = {60^0} + {30^0} = {90^0}\,\,\left( 3 \right)\).
Chứng minh tương tự ta có \(\widehat {ABD} = {90^0}\,\,\left( 4 \right).\)
Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) ta nhận được \(\widehat {ABD} + \widehat {DCA} = {90^0} + {90^0} = {180^0}\,.\)
Vậy tứ giác \(ABDC\) là tứ giác nội tiếp.
Hướng dẫn giải:
Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.