I. KIẾN THỨC CẦN NHỚ
- Cách làm tính trừ trong phạm vi ${\bf{4}}$
- Mối quan hệ giữa phép cộng và phép trừ.
- Biểu thị tình huống trong hình vẽ bằng phép tính và ứng dụng phép trừ vừa học vào các bài toán thực tế.
II. CÁC DẠNG TOÁN
Dạng 1: Thực hiện phép tính
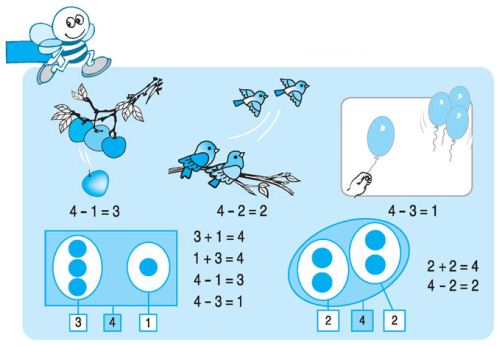
- Tính giá trị các phép trừ trong phạm vi \(4\).
Ví dụ: \(4 - 1 = ?\)
Cách 1: Nhẩm \(1+3=4\) nên \(4 - 1 = 3\)
Cách 2: Nhẩm từ \(4\) lùi về \(1\) đơn vị, được số nào thì đó là kết quả của phép tính \(4 - 1\)

Cách 3: Sử dụng hình ảnh để tìm kết quả của phép trừ: Có \(4\) cái bánh mà ăn mất một cái thì còn lại mấy cái ? Em gạch bớt một cái và đếm số bánh còn lại.
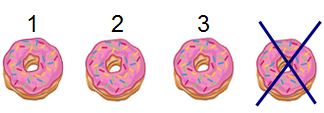
\(4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1 = \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\)
Số cần điền vào dấu hỏi chấm là \(3\)
Dạng 2: Tính giá trị của biểu thức có chứa nhiều phép tính cộng và trừ.
Biểu thức có chứa hai hoặc nhiều phép tính cộng, trừ thì em thực hiện các phép tính từ trái sang phải.
Ví dụ: \(4 - 1 - 2 = ......\)
Thực hiện phép tính \(4 - 1\) được kết quả bao nhiêu thì trừ tiếp cho \(2\)
\(4 - 1 - 2 = 3 - 2 = 1\)
Vậy số cần điền vào chỗ chấm là \(1\)
Dạng 3: So sánh
- Thực hiện phép tính của hai vế.
- So sánh và điền dấu thích hợp vào chỗ chấm.
Ví dụ: Điền dấu >; < hoặc = vào chỗ chấm:
\(4 - 1\,\,\,....\,\,\,3 + 2\)
Giải:
\(\begin{array}{l}4 - 1\,\,\, < \,\,\,3 + 2\\\,\,\,3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5\end{array}\)
Số cần điền vào chỗ chấm là dấu “<”

