Câu hỏi:
1 năm trước
Xem hệ cơ liên kết như hình vẽ, biết m1 = 3kg; m2 = 1kg; hệ số ma sát giữa vật và mặt phẳng nghiêng là \(\mu = 0,1\); \(\alpha = {30^ \circ };g = 10\left( {m/{s^2}} \right)\). Tính sức căng của dây?
Trả lời bởi giáo viên
Đáp án đúng: a
Phân tích các lực tác dụng ta có hình vẽ:
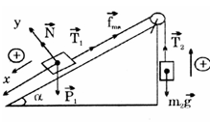
Chọn hệ trục Oxy như hình vẽ.
Giả thiết m1 trượt xuống mặt phẳng nghiêng và m2 đi lên, lúc đó hệ lực có chiều như hình vẽ. Vật chuyển động nhanh dần đều nên với chiều dương đã chọn, nếu ta tính được a > 0 thì chiều chuyển động đã giả thiết là đúng.
Áp dụng định luật II Newton cho vật I: \(\overrightarrow {{P_1}} + \overrightarrow N + \overrightarrow {{T_1}} + \overrightarrow {{F_{m{\rm{s}}}}} = {m_1}\overrightarrow {{a_1}} \)
Chiếu lên hệ tọa độ Ox ta được: \({m_1}g{\rm{sin}}\alpha - T - \mu N = ma\)(1)
Chiếu lên Oy ta có: \( - {m_1}gco{\rm{s}}\alpha {\rm{ + N = 0}}\)
thay vào (1) ta được: \({m_1}g\sin \alpha - T - \mu {m_1}gco{\rm{s}}\alpha {\rm{ = ma}}\)(2)
Áp dụng định luật II Newton cho vật II: \(\overrightarrow {{P_2}} + \overrightarrow {{T_2}} = {m_2}\overrightarrow {{a_2}} \)
chiếu lên hệ Oxy ta được: \( - {m_2}g + T = {m_2}a\)(3)
Cộng (2) và (3) ta được: \({m_1}g\sin \alpha - \mu {m_1}gco{\rm{s}}\alpha {\rm{ = }}\left( {{m_1} + {m_2}} \right)a\)
\(\begin{array}{l} \Rightarrow a = \dfrac{{{m_1}g\sin \alpha - \mu {m_1}co{\rm{s}}\alpha - {{\rm{m}}_2}g}}{{{m_1} + {m_2}}}\\ \Rightarrow a = \dfrac{{3.10.\dfrac{1}{2} - 0,1.3\dfrac{{\sqrt 3 }}{2} - 1.10}}{4} \approx 0,6\left( {m/{s^2}} \right)\end{array}\)
a > 0 nên chiều chuyển động giả sử là đúng
từ đó: \(T = {m_2}\left( {g + a} \right) = 1\left( {10 + 0,6} \right) = 10,6N\)
Hướng dẫn giải:
Phân tích các lực tác dụng lên vật
Chọn hệ tọa độ hoặc chiều dương
Viết hệ thức định luật II cho vật/hệ vật
Câu hỏi khác
- Đề kiểm tra học kì I - Đề số 5 - Sách chân trời sáng tạo có đáp án và lời giải chi tiết
- Đề kiểm tra học kì I - Đề số 1 - Sách chân trời sáng tạo có đáp án và lời giải chi tiết
- Đề kiểm tra học kì 1 - Đề số 2 - Sách chân trời sáng tạo có đáp án và lời giải chi tiết
- Đề kiểm tra học kì I - Đề số 4 - Sách chân trời sáng tạo có đáp án và lời giải chi tiết
- Đề kiểm tra học kì I - Đề số 4 - Sách chân trời sáng tạo có đáp án và lời giải chi tiết
