Câu hỏi:
2 năm trước
Từ mặt đất người ta ném một vật khối lượng 5kg lên cao theo phương thẳng đứng. Thời gian đạt độ cao cực đại là \({t_1}\), thời gian trở lại mặt đất là \({t_2}\). Biết \({t_1} = \dfrac{{{t_2}}}{2}\). Cho \(g = 10m/{s^2}\). Độ lớn lực cản không khí (xem như không đổi) có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: d
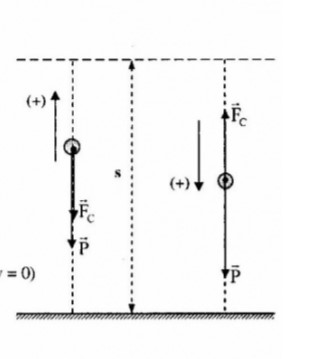
Các lực tác dụng lên vật : Trọng lực \(\overrightarrow P \) , lực cản của không khí \(\overrightarrow {{F_c}} \)
Phương trình chuyển động của vật là: \(\overrightarrow P + \overrightarrow {{F_c}} = m\overrightarrow a \) (1)
Khi vật đi lên : \(t = {t_1},a = {a_1}\)
+ Chiếu (1) lên phương thẳng đứng, chiều dương hướng lên ta được:
\( - p - {F_c} = m{a_1}\) \( \Rightarrow {a_1} = - g - \dfrac{{{F_c}}}{m}\) (2)
+ Gọi \({v_0}\) là vận tốc của vật ban đầu, s là độ cao cực đại mà vật đạt được, ta có:
\(\begin{array}{l}{v^2} - {v_0}^2 = 2{{\rm{a}}_1}s \Rightarrow {v_0} = \sqrt {2{\rm{s}}(g + \dfrac{{{F_c}}}{m}} )\\v = {v_0} + {a_1}{t_1} \to {t_1} = \dfrac{{ - {v_0}}}{{{a_1}}} = \dfrac{{2{\rm{s}}}}{{{v_0}}}\\ \Rightarrow {t_1} = \dfrac{{2{\rm{s}}}}{{\sqrt {2{\rm{s}}(g + \dfrac{{{F_c}}}{m}} )}}\end{array}\)
+ Khi vật đi xuống: \(t = {t_2},a = {a_2}\)
+ Chiếu (1) lên phương thẳng đứng, chiều dương hướng xuống ta được:
\(P - {F_c} = m{a_2} \to {a_2} = g - \dfrac{{{F_C}}}{m}(4)\)
Thời gian vật trở lại mặt đất:
\({t_2} = \sqrt {\dfrac{{2{\rm{s}}}}{{{a_2}}}} = \sqrt {\dfrac{{2{\rm{s}}}}{{g - \dfrac{{{F_C}}}{m}}}} \)
Mà \({t_1} = \dfrac{{{t_2}}}{2} \Rightarrow \dfrac{{2{\rm{s}}}}{{\sqrt {2{\rm{s}}(g + \dfrac{{{F_c}}}{m}} )}} = \dfrac{1}{2}\sqrt {\dfrac{{2{\rm{s}}}}{{g - \dfrac{{{F_C}}}{m}}}} \)
\(\begin{array}{l} \Rightarrow 4(g - \dfrac{{{F_C}}}{m}) = (g + \dfrac{{{F_c}}}{m})\\ \Rightarrow {F_C} = \dfrac{3}{5}mg = \dfrac{3}{5}.5.10 = 30N\end{array}\)
Vậy độ lớn của lực cản không khí là: \(30N\)
Hướng dẫn giải:
+ Vận dụng định luật II Niutơn: \(\overrightarrow F = m\overrightarrow a \)
+ Viết phương trình vận tốc của vật: $v = {v_0} + at$
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 2: động lực học chất điểm - đề số 04 Lý 10 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 2: động lực học chất điểm - đề số 02 Lý 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 2: động lực học chất điểm - đề số 02 Lý 10 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 2: động lực học chất điểm - đề số 03 Lý 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 2: động lực học chất điểm - đề số 03 Lý 10 có lời giải chi tiết
