Câu hỏi:
2 năm trước
Tứ giác $ABCD$ nội tiếp đường tròn có hai cạnh đối $AB$ và $CD$ cắt nhau tại $M$ và $\widehat {BAD} = {70^0}$ thì $\widehat {BCM} = ?$
Trả lời bởi giáo viên
Đáp án đúng: c
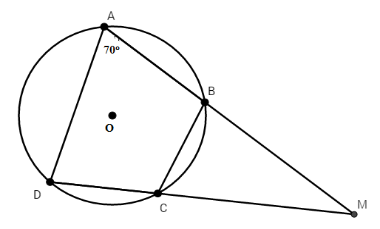
Tứ giác $ABCD$ nội tiếp nên có: $\widehat {DAB} + \widehat {BCD} = {180^0}$$ \Rightarrow \widehat {BCD} = {180^0} - {70^0} = {110^0}$
Mà $\widehat {BCD} + \widehat {BCM} = {180^0}$(kề bù) $ \Rightarrow \widehat {BCM} = {180^0} - {110^0} = {70^0}$
Hướng dẫn giải:
Áp dụng tính chất tứ giác nội tiếp có tổng hai góc đối diện bằng \({180^0}.\)
Giải thích thêm:
Các em có thể sử dụng tính chất : “ Trong một tứ giác nội tiếp góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó.”