Trong mặt phẳng Oxy, cho hình chữ nhật OABC với \(A\left( {0;10} \right),B\left( {100;10} \right),C\left( {100;0} \right)\). Gọi S là tập hợp tất cả các điểm nằm bên trong (kể cả trên cạnh) của hình chữ nhật OABC. Số phần tử của S bằng
Chỉ điền số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
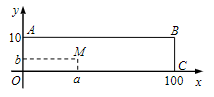
Số phần tử của S là số cặp \(\left( {a;b} \right)\)
Điểm \(M\left( {a;b} \right)\) nằm bên trong hình chữ nhật OABC (tính cả trên cạnh) nên ta có:
Vì \(a \in \mathbb{Z}\) và \(0 \le a \le 100\) => a có 101 cách chọn
Vì \(b \in \mathbb{Z}\) và \(0 \le b \le 10\) => b có 11 cách chọn
Theo quy tắc nhân, số cặp \(\left( {a;b} \right)\) thỏa yêu cầu bài toán là \(101.11 = 1111\).
Suy ra S có 1111 phần tử.
Hướng dẫn giải:
- Số phần tử của S là số cặp \(\left( {a;b} \right)\)
- Tìm số cách chọn a và b
- Sử dụng quy tắc nhân chọn số cặp \(\left( {a;b} \right)\)



