Trong không gian \(Oxyz,\) cho \(A\left( {0;0;2} \right),\,\,B\left( {1;1;0} \right)\) và mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {\left( {z - 1} \right)^2} = \dfrac{1}{4}\). Xét điểm \(M\) thay đổi thuộc \(\left( S \right)\). Giá trị nhỏ nhất của biểu thức \(M{A^2} + 2M{B^2}\) bằng:

Gọi \(I\left( {a;b;c} \right)\) là điểm thỏa mãn \(\overrightarrow {IA}  + 2\overrightarrow {IB}  = \overrightarrow 0 \) ta có:

\(\begin{array}{l} \Rightarrow \left( { - a; - b;2 - c} \right) + 2\left( {1 - a;1 - b; - c} \right) = 0\\ \Leftrightarrow \left\{ \begin{array}{l} - a + 2 - 2a = 0\\ - b + 2 - 2b = 0\\2 - c - 2c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{2}{3}\\b = \dfrac{2}{3}\\c = \dfrac{2}{3}\end{array} \right. \Rightarrow I\left( {\dfrac{2}{3};\dfrac{2}{3};\dfrac{2}{3}} \right)\end{array}\)

Ta có:

\(\begin{array}{l}M{A^2} + 2M{B^2} = {\left( {\overrightarrow {MI}  + \overrightarrow {IA} } \right)^2} + 2{\left( {\overrightarrow {MI}  + \overrightarrow {IB} } \right)^2}\\ = M{I^2} + 2\overrightarrow {MI} \overrightarrow {IA}  + I{A^2} + 2M{I^2} + 4\overrightarrow {MI} .\overrightarrow {IB}  + I{B^2}\\ = 3M{I^2} + I{A^2} + 2I{B^2} + 2\overrightarrow {MI} \underbrace {\left( {\overrightarrow {IA}  + 2\overrightarrow {IB} } \right)}_{\overrightarrow 0 } = 3M{I^2} + \underbrace {I{A^2} + 2I{B^2}}_{const}\end{array}\)

Do \(\left\{ \begin{array}{l}I{A^2} = {\left( {\dfrac{{ - 2}}{3}} \right)^2} + {\left( {\dfrac{{ - 2}}{3}} \right)^2} + {\left( {2 - \dfrac{2}{3}} \right)^2} = \dfrac{8}{3}\\I{B^2} = {\left( {1 - \dfrac{2}{3}} \right)^2} + {\left( {1 - \dfrac{2}{3}} \right)^2} + {\left( {\dfrac{{ - 2}}{3}} \right)^2} = \dfrac{2}{3}\end{array} \right. \Rightarrow I{A^2} + 2I{B^2} = 4\) không đổi \( \Rightarrow {\left( {M{A^2} + 2M{B^2}} \right)_{\min }} \Leftrightarrow M{I_{\min }}\) với \(I\left( {\dfrac{2}{3};\dfrac{2}{3};\dfrac{2}{3}} \right),\,\,M \in \left( S \right)\).

Ta có \({\left( {\dfrac{2}{3}} \right)^2} + {\left( {\dfrac{2}{3}} \right)^2} + {\left( {\dfrac{2}{3} - 1} \right)^2} = 1 > \dfrac{1}{4} \Rightarrow I\) nằm ngoài \(\left( S \right)\) .

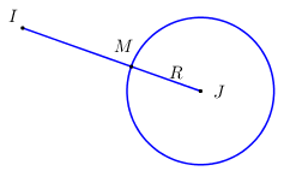
Vậy \({\left( {M{A^2} + 2M{B^2}} \right)_{\min }} = 3MI_{\min }^2 + 4 = 3.{\left( {\dfrac{1}{2}} \right)^2} + 4 = \dfrac{{19}}{4}\).