Trên đường tròn lượng giác gốc \(A\), cung lượng giác nào có các điểm biểu diễn tạo thành tam giác đều ?
Trả lời bởi giáo viên
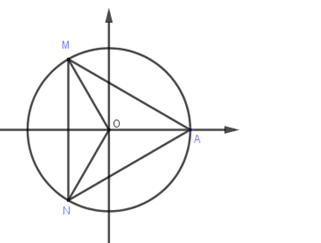
Đáp án A : Cung lượng giác có số đo \(\dfrac{{k2\pi }}{3}\).
- Với \(k = 1 \Rightarrow \dfrac{{1.2\pi }}{3} = \dfrac{{2\pi }}{3}\) ta có điểm \(M\).
- Với \(k = 2 \Rightarrow \dfrac{{k2\pi }}{3} = \dfrac{{4\pi }}{3}\) ta có điểm \(N\).
- Với \(k = 3 \Rightarrow \dfrac{{k2\pi }}{3} = 2\pi \) ta có điểm \(A\).
- Với \(k = 4 \Rightarrow \dfrac{{k2\pi }}{3} = \dfrac{{8\pi }}{3} = 2\pi + \dfrac{{2\pi }}{3}\) có điểm biểu diễn \(M\).
Tương tự với các giá trị khác của \(k\) ta cũng chie thu được \(3\) điểm \(M,N,A\) trên đường tròn lượng giác và ba điểm đó tạo thành một tam giác đều nên A thỏa mãn.
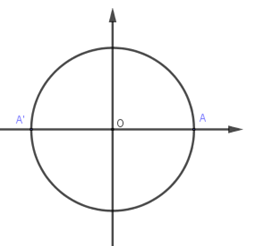
Đáp án B : Chỉ có hai điểm biểu diễn là \(A\) và \(A'\) nên loại B.
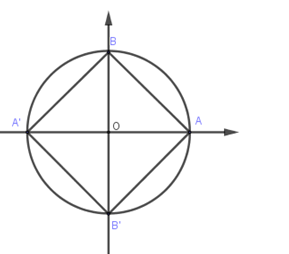
Đáp án C : Có \(4\) điểm biểu diễn \(A,A',B,B'\) tạo thành hình vuông nên loại C.
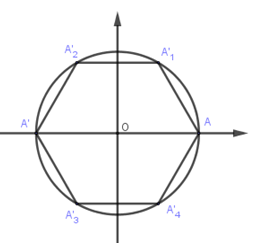
Đáp án D : Có \(6\) điểm biểu diễn tạo thành hình lục giác đều nên loại D.
Hướng dẫn giải:
- Tìm các điểm biểu diễn mỗi cung lượng giác ở từng đáp án rồi đối chiếu kết quả.
Phương pháp tìm điểm biểu diễn:
Cho \(k\) lần lượt các giá trị \(1,2,3,4,...\) và tìm điểm biểu diễn của cung đó trên đường tròn lượng giác.
Giải thích thêm:
Một phương pháp khác để loại trừ đáp án trong bài toán này là các em có thể tính số điểm biểu diễn bằng cách lấy \(k2\pi \) chia cho từng phần có chứa \(k\).
Chảng hạn: Góc lượng giác \(\dfrac{\pi }{3} + \dfrac{{k\pi }}{2}\) thì có \(\left( {k2\pi } \right):\left( {\dfrac{{k\pi }}{2}} \right) = 4\) điểm biểu diễn.

