Tìm tất cả các giá trị thực thuộc đoạn [-2;2] của tham số m để bất phương trình \(4{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0\) nghiệm đúng với mọi giá trị \(x \in \left( {1;64} \right)\).
Chỉ điền số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Ta có: \(4{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0\)
\( \Leftrightarrow {\left( {{{\log }_2}x} \right)^2} + {\log _2}x + m \ge 0\)
Đặt \(t = {\log _2}x\), khi \(x \in \left( {1;64} \right)\) thì \(t \in \left( {0;6} \right)\)
Suy ra \({t^2} + t + m \ge 0 \Leftrightarrow m \ge - {t^2} - t\left( * \right)\)
Hàm số \(f\left( t \right) = - {t^2} - t\) với \(t \in \left( {0;6} \right)\)
Ta có: \(f'\left( t \right) = - 2t - 1 < 0,\forall t \in \left( {0;6} \right)\)
Bảng biến thiên:
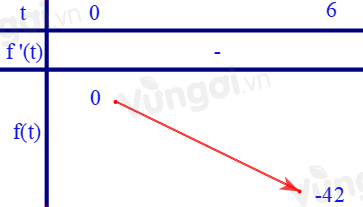
Bất phương trình đã cho đúng với mọi \(x \in \left( {1;64} \right)\) khi và chỉ khi bất phương trình (*) đúng với mọi \(t \in \left( {0;6} \right)\)\( \Leftrightarrow m \ge 0\)
Mà \(m \in \left[ { - 2;2} \right] \Rightarrow m \in \left[ {0;2} \right]\)
Vậy có 3 giá trị nguyên của m thỏa mãn bài toán.
Hướng dẫn giải:
- Đưa về bất phương trình cùng cơ số
- Đặt \(t = {\log _2}x\), tìm điều kiện của t.
- Đưa bất phương trình về bậc hai ẩn t
- Lập bảng biến thiên của hàm f(t)
- Tìm m
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
