Trả lời bởi giáo viên
Đáp án đúng: d
Vì 525⋮a;875⋮a;280⋮a và a là số lớn nhất⇒a=ƯCLN(525;875;280)
Ta có:
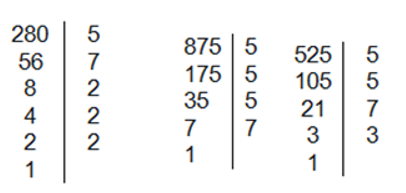
Nên 525=3.52.7;875=53.7;280=23.5.7
⇒a= ƯCLN(525;875;280)=5.7=35
Hướng dẫn giải:
Ta đưa về bài toán tìm ƯCLN của 525;875;280.
Bước 1: Phân tích 525;875;280 ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Lập tích các thừa số nguyên tố chung đó, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
Đó chính là số cần tìm.

