Câu hỏi:
2 năm trước
Thanh MN chiều dài \(l{\rm{ }} = {\rm{ }}20cm\) quay đều quanh trục qua M và vuông góc với thanh trong từ trường đều \(B = 0,04T\) làm thanh xuất hiện suất điện động cảm ứng \(e_C = {\rm{ }}0,4V\).
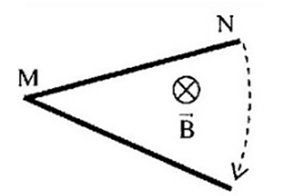
Tốc độ góc của thanh là:
Trả lời bởi giáo viên
Đáp án đúng: a
Xét trong khoảng thời gian ∆t, thanh quét được diện tích:
\(\Delta S = \pi {l^2}\dfrac{{\Delta \varphi }}{{2\pi }} = \pi {l^2}\dfrac{{\omega \Delta t}}{{2\pi }} = \dfrac{{{l^2}\omega }}{2}\Delta t\)
Độ biến thiên từ thông : \(\Delta \Phi = B\Delta Sc{\rm{os}}\alpha = B\Delta S\) ( vì \(\cos \alpha = 1\))
+ Suất điện động cảm ứng:
\(\begin{array}{l}\left| {{e_C}} \right| = \dfrac{{\Delta \Phi }}{{\Delta t}} = \dfrac{{B\Delta S}}{{\Delta t}} = \dfrac{{B\dfrac{{{l^2}\omega }}{2}\Delta t}}{{\Delta t}} = \dfrac{{B{l^2}\omega }}{2}\\ \to \omega = \dfrac{{2e_C}}{{B{l^2}}} = \dfrac{{2.0,4}}{{0,04.{{(0,2)}^2}}} = 500(ra{\rm{d/s)}}\end{array}\)
Hướng dẫn giải:
Vận dụng biểu thức tính suất điện động cảm ứng: \(\left| {{e_C}} \right| = \dfrac{{\Delta \Phi }}{{\Delta t}}\)
