Thả nổi trên mặt nước một đĩa nhẹ, chắn sáng, hình tròn. Mắt người quan sát đặt trên mặt nước sẽ không thấy được vật sáng ở đáy chậu khi bán kính đĩa không nhỏ hơn \(10 cm\). Tính chiều sâu của lớp nước trong chậu. Biết rằng vật và tâm đĩa nằm trên đường thẳng đứng và chiết suất của nước là \(n =\dfrac{4}{3}\).
Trả lời bởi giáo viên
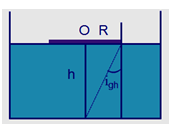
Ta có, góc giới hạn được xác định bởi biểu thức: \(\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{1}{n}\)
Từ hình, ta có: \(\sin {i_{gh}} = \dfrac{R}{{\sqrt {{R^2} + {h^2}} }}\)
\(\begin{array}{l} \Rightarrow \dfrac{1}{n} = \dfrac{R}{{\sqrt {{R^2} + {h^2}} }}\\ \Leftrightarrow \dfrac{3}{4} = \dfrac{{10}}{{\sqrt {{{10}^2} + {h^2}} }}\\ \Rightarrow h = 8,82cm\end{array}\)
Hướng dẫn giải:
+ Sử dụng hệ thức lượng giác trong tam giác
+ Vận dụng biểu thức tính góc giới hạn: \(\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}}\)

