Tập hợp tất cả các giá trị của tham số m để phương trình \(x\left( {x - 1} \right)\left( {x + 1} \right)\left( {x + 2} \right) = m\) có nghiệm thuộc đoạn \(\left[ {0;1} \right]\) là:
Trả lời bởi giáo viên
Xét hàm số \(f\left( x \right) = x\left( {x - 1} \right)\left( {x + 1} \right)\left( {x + 2} \right) = {x^4} + 2{x^3} - {x^2} - 2x\)
TXĐ: \(D = R\). Ta có \(f'\left( x \right) = 4{x^3} + 6{x^2} - 2x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\\x = \frac{{ - 1 - \sqrt 5 }}{2}\\x = \frac{{ - 1 + \sqrt 5 }}{2}\end{array} \right.\).
BBT:
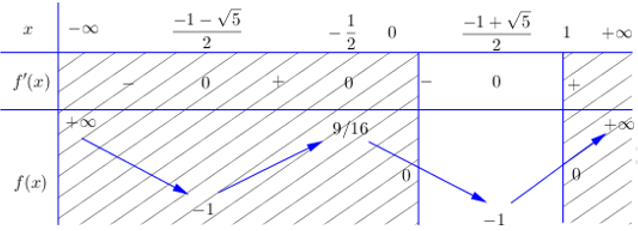
Từ BBT ta thấy phương trình có nghiệm thuộc \(\left[ {0;1} \right] \Leftrightarrow m \in \left[ { - 1;0} \right]\).
Hướng dẫn giải:
Số nghiệm của phương trình \(x\left( {x - 1} \right)\left( {x + 1} \right)\left( {x + 2} \right) = m\) là số giao điểm của đồ thị hàm số \(f\left( x \right) = x\left( {x - 1} \right)\left( {x + 1} \right)\left( {x + 2} \right)\) và đường thẳng \(y = m\).



