Tại ba đỉnh của tam giác đều \(ABC\), cạnh \(a = 10cm\) có ba điện tích điểm bằng nhau và bằng \(10nC\). Hãy xác định cường độ điện trường tại trung điểm của cạnh AB.

Gọi \(H\) - trung điểm của cạnh \(AB\)

Gọi \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) lần lượt là cường độ điện trường do điện tích \({q_1},{q_2},{q_3}\) gây ra tại \(H\)

Ta có, các véc-tơ \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) được biểu diễn như hình

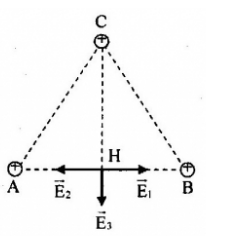
Ta có: \({E_1} = {E_2} = k\dfrac{{\left| q \right|}}{{{{\left( {\dfrac{{AB}}{2}} \right)}^2}}}\)

\({E_3} = k\dfrac{{\left| q \right|}}{{C{H^2}}}\)

Lại có:

\(\begin{array}{l}CH = \sqrt {C{B^2} - B{H^2}}  = \sqrt {C{B^2} - {{\left( {\dfrac{{AB}}{2}} \right)}^2}} \\ = \sqrt {{{10}^2} - \dfrac{{{{10}^2}}}{4}}  = 5\sqrt 3 cm\end{array}\)

Ta suy ra: \({E_3} = {9.10^9}\dfrac{{{{10.10}^{ - 9}}}}{{{{\left( {5\sqrt 3 {{.10}^{ - 2}}} \right)}^2}}} = 12000V/m\)

Ta có, cường độ điện trường tổng hợp tại \(H\): \(\overrightarrow E  = \overrightarrow {{E_1}}  + \overrightarrow {{E_2}}  + \overrightarrow {{E_3}} \)

Vì \(\left\{ \begin{array}{l}\overrightarrow {{E_1}}  \uparrow  \downarrow \overrightarrow {{E_2}} \\{E_1} = {E_2}\end{array} \right. \Rightarrow \overrightarrow {{E_{12}}}  = \overrightarrow {{E_1}}  + \overrightarrow {{E_2}}  = \overrightarrow 0 \)

Ta suy ra: \(\overrightarrow E  = \overrightarrow {{E_3}} \)

\( \Rightarrow E = {E_3} = 12000V/m\)