Người ta có nhiều nguồn âm điểm giống hệt nhau và cùng công suất. Ban đầu tại điểm O đặt 2 nguồn âm. Điểm A cách O một khoảng d có thể thay đổi được. Trên tia vuông góc với OA tại A, lấy điểm B cách A khoảng 6cm. Điểm M nằm trong đoạn AB sao cho AM=4,5cm và góc MOB có giá trị lớn nhất, lúc này mức cường độ âm tại A là L_A=40dB. Cần phải đặt thêm tại O bao nhiêu nguồn nữa để mức cường độ âm tại M là 50dB.

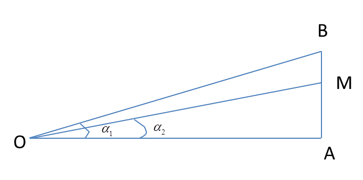
OA = d m

AB = 6 m

AM = 4,5 m

\(\begin{gathered}\tan  = \tan ({\alpha _1} - {\alpha _2}) = \dfrac{{\tan {\alpha _1} - \tan {\alpha _2}}}{{1 +\tan {\alpha _1}\tan {\alpha _2}}} \hfill \\= \dfrac{{\dfrac{6}{d} - \dfrac{{4,5}}{d}}}{{1 + \dfrac{6}{d}.\dfrac{{4,5}}{d}}} = \dfrac{{1,5}}{{d + \dfrac{{27}}{d}}} \hfill \\\end{gathered} \)

Theo BĐT Cosi, ta có:

\(\begin{gathered}d + \dfrac{{27}}{d} \geqslant 2\sqrt {27}  = 2.3\sqrt 3  \hfill \\\to d = 3\sqrt 3 m \hfill \\ \end{gathered} \)

Do đó:

$OM = \sqrt {{{(3\sqrt 3 )}^2} + 4,{5^2}}  = \dfrac{{3\sqrt {21} }}{2}m$

Ta có:

\({L_A} - {L_M} = 10\log \dfrac{{{I_A}}}{{{I_M}}} \leftrightarrow 40 - 50 =  - 10 = 10\log \dfrac{{{I_A}}}{{{I_M}}} \to \dfrac{{{I_A}}}{{{I_M}}} = 0,1\)

Mặt khác:

$\begin{gathered}\left\{ \begin{gathered}{I_A} = \dfrac{{2P}}{{4\pi R_A^2}} \hfill \\{I_M} = \dfrac{{(x + 2)P}}{{4\pi R_M^2}} \hfill \\\end{gathered}  \right. \to \frac{{{I_A}}}{{{I_M}}} = \dfrac{2}{{x + 2}}\frac{{R_M^2}}{{R_A^2}} = \dfrac{2}{{x + 2}}\dfrac{{{{(\dfrac{{3\sqrt {21} }}{2})}^2}}}{{{{(3\sqrt 3 )}^2}}} = 0,1\hfill \\\to x = 33 \hfill \\\end{gathered} $