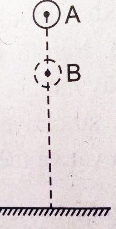
Một vật rơi từ vị trí A xuống mặt đất. Bỏ qua sức cản không khí. Khi vật rơi đến vị trí B thì động năng của vật bằng \(\dfrac{1}{3}\) thế năng của nó. Động năng của vật tiếp tục tăng thêm một lượng là \(60J\) thì có giá trị bằng thế năng. Thế năng của vật ở vị trí A là:

Gọi \({{\rm{W}}_d},{{\rm{W}}_t},{\rm{W}}\) lần lượt là động năng, thế năng và cơ năng của vật

C – là vị trí có động năng bằng thế năng

Theo đề bài, ta có:

+ Tại B: \({{\rm{W}}_{{d_B}}} = \dfrac{1}{3}{{\rm{W}}_{{t_B}}} \to 3{{\rm{W}}_{{d_B}}} = {{\rm{W}}_{{t_B}}}\)

 + Tại C: \(\left\{ \begin{array}{l}{{\rm{W}}_{{d_C}}} = {{\rm{W}}_{{d_B}}} + 60\\{{\rm{W}}_{{t_C}}} = {{\rm{W}}_{{t_B}}} - 60 = 3{W_{{d_B}}} - 60\end{array} \right.\)

Lại có:

\(\begin{array}{l}{{\rm{W}}_{{d_C}}} = {{\rm{W}}_{{t_C}}} \leftrightarrow {{\rm{W}}_{{d_B}}} + 60 = 3{{\rm{W}}_{{d_B}}} - 60\\ \to {{\rm{W}}_{{d_B}}} = 60J\end{array}\)

Thế vào (1), ta suy ra: \({{\rm{W}}_{{t_B}}} = 3.60 = 180J\)

Áp dụng định luật bảo toàn và chuyển hóa năng lượng, ta có:

Cơ năng của vật tại B: \({{\rm{W}}_B} = {{\rm{W}}_{{d_B}}} + {{\rm{W}}_{{t_B}}} = 60 + 180 = 240J\)

Thế năng của vật tại A bằng cơ năng của vật tại B

(do tại A vật chỉ có thế năng mà không có động năng)

\({{\rm{W}}_{{t_A}}} = {{\rm{W}}_B} = 240J\)