Một vật nhỏ dao động điều hòa với chu kì $T$ và biên độ $8 cm$. Biết trong một chu kì, khoảng thời gian để vật nhỏ có độ lớn vận tốc không vượt quá $16 cm/s$ là $\dfrac{T}{3}$. Tần số góc của dao động là:
Một vật nhỏ dao động điều hòa với chu kì $T$ và biên độ $8 cm$. Biết trong một chu kì, khoảng thời gian để vật nhỏ có độ lớn vận tốc không vượt quá $16 cm/s$ là $\dfrac{T}{3}$. Tần số góc của dao động là:
Trả lời bởi giáo viên
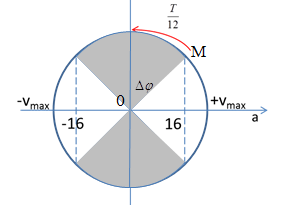
Khoảng thời gian \(\dfrac{T}{3}\) ứng với vùng màu xám trong hình trên
Ta suy ra: Khoảng thời gian vận tốc biến thiên từ 0 đến vị trí vận tốc có độ lớn \(16cm/{s^2}\) là: \(\Delta t = \dfrac{{\dfrac{T}{3}}}{4} = \dfrac{T}{{12}}\)
Cách 1:
=> Vị trí \(\left| v \right| = 16cm/s = \dfrac{{{v_{{\rm{max}}}}}}{2} \to {v_{{\rm{max}}}} = 2v \leftrightarrow A\omega = 2v \to \omega = \dfrac{{2v}}{A} = \frac{{2.16}}{8} = 4{\rm{r}}a{\rm{d}}/s\)
Cách 2:
Từ vòng tròn lượng giác, ta có góc quét \(\Delta \varphi = \omega .\Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{{12}} = \dfrac{\pi }{6}rad\)
\(\begin{array}{l}OM.\sin \Delta \varphi = 16\\ \leftrightarrow A\omega .\sin \Delta \varphi = 16\\ \to \omega = \dfrac{{16}}{{A.\sin \Delta \varphi }} = \dfrac{{16}}{{8.\sin \dfrac{\pi }{6}}} = 4\left( {rad/s} \right)\end{array}\)
Hướng dẫn giải:
+ Sử dụng vòng tròn lượng giác và thời gian trên đường thẳng được suy ra từ đường tròn
+ Sử dụng công thức tính vận tốc cực đại: vmax = Aω

