Câu hỏi:
1 năm trước
Một vật chuyển động thẳng có phương trình \(x = 30 + 4t - {t^2}(m;s)\) . Tính quãng đường vật đi từ thời điểm $t_1 = 1s$ đến thời điểm $t_2 = 3s$?
Trả lời bởi giáo viên
Đáp án đúng: a
Từ phương trình tọa độ - thời gian ta thu được phương trình vận tốc \(v = 4 - 2t \to v = 0 \leftrightarrow t = 2{\rm{s}}\) , vật sẽ đổi chiều chuyển động sau $2s$.
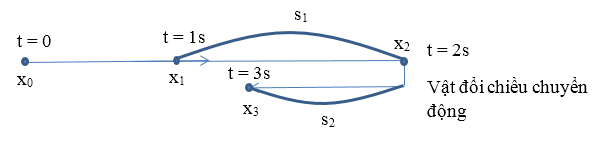
Do vậy quãng đường đi được của vật được tính:
\(s = {s_1} + {s_2} = \left| {{x_2} - {x_1}} \right| + \left| {{x_3} - {x_2}} \right| = \left| {4 - 3} \right| + \left| {3 - 4} \right| = 2m\)
Hướng dẫn giải:
+ Xác định xem trong khoảng thời gian \(\Delta t\) vật có đổi chiều không
+ Thay t vào phương trình chuyển động để xác định quãng đường
Câu hỏi khác
- Đề kiểm tra học kì I - Đề số 5 - Sách chân trời sáng tạo có đáp án và lời giải chi tiết
- Đề kiểm tra học kì I - Đề số 1 - Sách chân trời sáng tạo có đáp án và lời giải chi tiết
- Đề kiểm tra học kì 1 - Đề số 2 - Sách chân trời sáng tạo có đáp án và lời giải chi tiết
- Đề kiểm tra học kì I - Đề số 4 - Sách chân trời sáng tạo có đáp án và lời giải chi tiết
- Đề kiểm tra học kì I - Đề số 4 - Sách chân trời sáng tạo có đáp án và lời giải chi tiết
