Câu hỏi:
2 năm trước
Một tia sáng được chiếu đến điểm chính giữa của mặt trên một khối hình hộp chữ nhật trong suốt trong mặt phẳng hình chéo như hình, chiết suất n = 1,5. Xác định góc tới lớn nhất để tia khúc xạ còn gặp mặt đáy của khối hộp chữ nhật? Biết \(AB = a\), \(AA' = AD = 2a\).
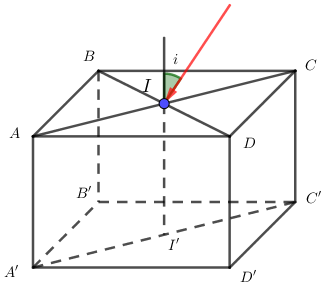
Trả lời bởi giáo viên
Đáp án đúng: c
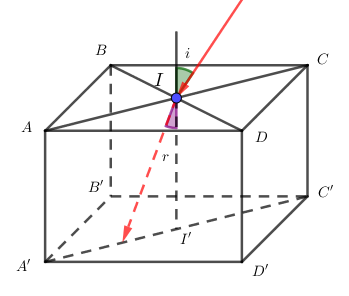
Theo định luật khúc xạ ánh sáng, ta có: \(1.\sin i = n{\mathop{\rm s}\nolimits} {\rm{inr}}\)
Khi \({i_{max}}\) thì \({r_{max}}\)
Ta có, \({r_{max}}\) khi tia khúc xạ đến một điểm A’ của đáy hình hộp.
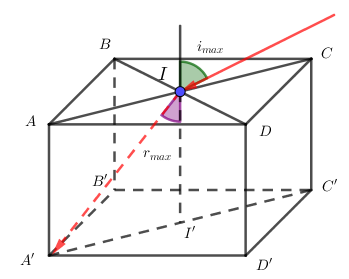
Từ hình, ta có:
\({\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{{\rm{max}}}} = \dfrac{{I'A'}}{{IA'}}\)
Lại có: \(\left\{ \begin{array}{l}A'I' = \dfrac{{A'C'}}{2} = \dfrac{{a\sqrt 5 }}{2}\\IA' = \sqrt {AA{'^2} + A'I{'^2}} = \sqrt {4{a^2} + \dfrac{{5{a^2}}}{4}} = \dfrac{{\sqrt {21} a}}{2}\end{array} \right.\)
Ta suy ra: \({\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{\max }} = \dfrac{{\dfrac{{a\sqrt 5 }}{2}}}{{\dfrac{{\sqrt {21} a}}{2}}} = \sqrt {\dfrac{5}{{21}}} \)
\(\begin{array}{l} \Rightarrow \sin {i_{{\rm{max}}}} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{{\rm{max}}}} = 1,5.\sqrt {\dfrac{5}{{21}}} \\ \Rightarrow {i_{{\rm{max}}}} = {47^0}\end{array}\)
Hướng dẫn giải:
+ Vẽ đường truyền của tia sáng trong khối lập phương
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
+ Sử dụng hệ thức lượng giác
