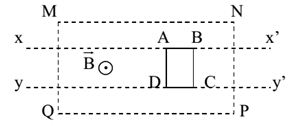
Một thanh dẫn điện dài \(20{\rm{ }}\left( {cm} \right)\) được nối hai đầu của nó với hai đầu của một mạch điện có điện trở \(0,5\Omega \). Cho thanh chuyển động tịnh tiến trong từ trường đều cảm ứng từ \(B = 0,08\left( T \right)\) với vận tốc \(7{\rm{ }}\left( {m/s} \right)\), vectơ vận tốc vuông góc với các đường sức từ và vuông góc với thanh, bỏ qua điện trở của thanh và các dây nối. Cường độ dòng điện trong mạch là:

Dòng điện chạy trong khối vật dẫn

Dòng điện cảm ứng sinh ra trong mạch kín khi từ thông qua mạch biến thiên

Dòng điện cảm ứng sinh ra trong khối vật dẫn khi vật dẫn chuyển động trong từ trường.

Dòng điện xuất hiện trong tấm kim loại khi nối tấm kim loại với hai cực của nguồn điện

Khung đang chuyển động ở ngoài vùng MNPQ

Khung đang chuyển động ở trong vùng MNPQ

Khung đang chuyển động ở ngoài vào trong vùng MNPQ

Khung đang chuyển động đến gần vùng MNPQ

Đèn (1) sáng ngay lập tức, đèn (2) sáng từ từ

Đèn (1) và đèn (2) đều sáng lên ngay

Đèn (1) và đèn (2) đều sáng từ từ

Đèn (2) sáng ngay lập tức, đèn (1) sáng từ từ

Dòng điện cảm ứng được sinh ra trong khối vật dẫn khi chuyển động trong từ trường hay đặt trong từ trường biến đổi theo thời gian gọi là dòng điện Fu-cô

Dòng điện xuất hiện khi có sự biến thiên từ thông qua mạch điện kín gọi là dòng điện cảm ứng

Dòng điện Fu-cô được sinh ra khi khối kim loại chuyển động trong từ trường, có tác dụng chống lại chuyển động của khối kim loại đó.

Dòng điện Fu-cô chỉ được sinh ra khi khối vật dẫn chuyển động trong từ trường, đồng thời tỏa nhiệt làm cho khối vật dẫn nóng lên.

Đặc trưng cho từ trường về phương diện tác dụng lực từ.

Trùng với hướng của từ trường.

Có đơn vị là Tesla.

Phụ thuộc vào chiều dài đoạn dây dẫn mang dòng điện.