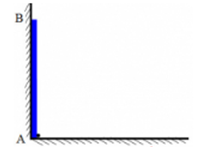
Một thanh cứng, mảnh $AB$ có chiều dài \(l = 2m\) dựng đứng sát bức tường thẳng đứng như hình. Ở đầu $A$ của thanh có một con kiến. Khi đầu $A$ của thanh bắt đầu chuyển động trên sàn ngang về bên phải theo phương vuông góc với bức tường thì con kiến cũng bắt đầu bò dọc theo thanh. Đầu $A$ chuyển động thẳng đều với vận tốc \({v_1} = 0,5cm/s\) so với sàn kể từ vị trí tiếp xúc với bức tường. Con kiến bò thẳng đều với vận tốc \({v_2} = 0,2cm/s\) so với thanh kể từ đầu $A$. Độ cao cực đại của con kiến đối với sàn ngang là bao nhiêu? Biết rằng đầu B của thanh luôn tiếp xúc với tường.
Trả lời bởi giáo viên
Ta có:
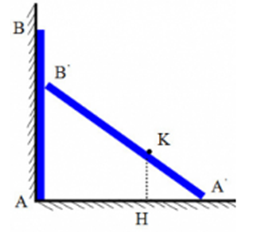
+ Khi đầu $A$ của thanh di chuyển từ $A$ đến $A’$ thì con kiến di chuyển từ $A’$ đến $K$ trong cùng một khoảng thời gian.
+ Khi đó: \(\dfrac{{{s_{{\rm{AA'}}}}}}{{{v_1}}} = \dfrac{{{s_{A'K}}}}{{{v_2}}} \to \dfrac{{{s_{{\rm{AA'}}}}}}{{{s_{A'K}}}} = \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{0,5}}{{0,2}} = 2,5\)
=> Nếu quãng đường con kiến di chuyển là \({s_{A'K}} = x \to {s_{AA'}} = 2,5x\)
Từ hình, ta có:
\({\left( {AB'} \right)^2} = {2^2} - {\left( {2,5{\rm{x}}} \right)^2} = 4 - 6,25{{\rm{x}}^2}\)
Mặt khác, ta có:
\(\begin{array}{l}\Delta A'KH \sim \Delta A'B'A\\ \to \dfrac{{HK}}{{AB'}} = \dfrac{{A'K}}{{A'B'}}\\ \to H{K^2} = {\left( {AB'} \right)^2}{\left( {\dfrac{{A'K}}{{A'B'}}} \right)^2} = (4 - 6,25{{\rm{x}}^2})\dfrac{{x{}^2}}{4} = - 1,5625{{\rm{x}}^4} + {x^2}\end{array}\)
Để HK có giá trị cực đại thì: \({x^2} = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{1}{{2.1,5625}} = 0,32\)
Khi đó: \(H{K_{{\rm{max}}}} = \sqrt { - 1,5625.0,{{32}^2} + 0,32} = 0,4(m)\)

