Một sóng điện từ lan truyền trong chân không dọc theo đường thẳng từ điểm M đến điểm N cách nhau \(45 m\). Biết sóng này có thành phần điện trường tại mỗi điểm biến thiên điều hòa theo thời gian với tần số \(5 MHz\). Lấy \(c = 3.10^8m/s\). Ở thời điểm t, cường độ điện trường tại M bằng \(0\). Thời điểm nào sau đây cường độ điện trường tại N bằng \(0\)?
Trả lời bởi giáo viên
Ta có:
+ Chu kì dao động của sóng: \(T = \dfrac{1}{f} = \dfrac{1}{{{{5.10}^6}}} = {2.10^{-7}}s\)
+ Độ lệch pha giữa M và N là: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi .d}}{{cT}} = \dfrac{{2\pi .45}}{{{{3.10}^8}{{.2.10}^{ - 7}}}} = \dfrac{{3\pi }}{2}\)
Vẽ trên vòng tròn lượng giác ta được:
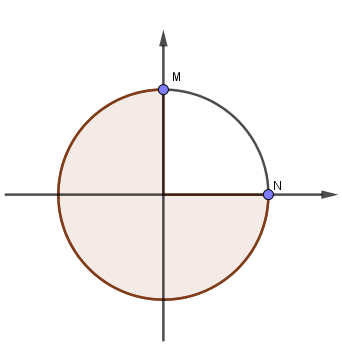
=> thời gian ngắn nhất để cường độ điện trường tại N bằng 0 là: \(\dfrac{T}{4} = \dfrac{{{{2.10}^{ - 7}}}}{4} = {50.10^{ - 9}} = 50ns\)
=> Thời điểm mà cường độ điện trường tại N bằng 0 là: \(t' = t + \left( {2n + 1} \right)\dfrac{T}{4}\) với n là số nguyên
Thay vào các phương án ta suy ra đáp án D
Hướng dẫn giải:
+ Vận dụng biểu thức tính chu kì dao động: \(T = \dfrac{1}{f}\)
+ Vận dụng biểu thức tính độ lệch pha giữa hai điểm trên phương truyền sóng: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
+ Sử dụng biểu thức tính bước sóng: \(\lambda = cT = \dfrac{c}{f}\)
+ Sử dụng vòng tròn lượng giác

