Câu hỏi:
2 năm trước
Một nguồn điện có suất điện động 3V, điện trở trong $2\Omega $, được mắc vào hai đầu mạch gồm một cuộn dây có điện trở thuần $3\Omega $ mắc song song với một tụ điện. Biết điện dung của tụ là $5\mu F$ và độ tự cảm là $5\mu H$ . Khi dòng điện chạy qua mạch đã ổn định, người ta ngắt nguồn điện khỏi mạch. Lúc đó nhiệt lượng lớn nhất toả ra trên cuộn dây bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: b
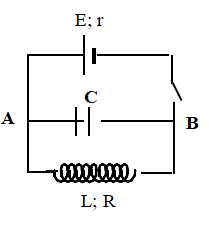
Khi dòng điện qua mạch ổn định (qua cuộn dây):
\(I = \frac{E}{{{r_n} + {r_d}}} = \frac{3}{5}(A)\) ( Hay: I = E /(R + r) = 3/5 = 0,6 (A))
Hiệu điện thế ở hai đầu cuộn dây cũng chính là hiệu điện thế giữa 2 đầu tụ:
UAB = U0 = IR = 1,8 (V)
Năng lượng dao động của mạch lúc ngắt nguồn: \(W = \frac{1}{2}L{I^2} + \frac{1}{2}C{U^2} = 4,{5.10^{ - 6}}(J)\)
Nhiệt lượng lớn nhất tỏa ra trên cuộn dây bằng (W )năng lượng dao động lúc đầu của mạch
Lúc đó nhiệt lượng lớn nhất toả ra trên cuộn dây bằng năng lượng của mạch khi đó
\({Q_{max}} = W = \frac{{CU_0^2}}{2} + \frac{{L{I^2}}}{2} = {\rm{ }}8,{1.10^{ - 6}} + {\rm{ }}0,{9.10^{ - 6}} = {\rm{ }}{9.10^{ - 6{\rm{ }}}}(J){\rm{ }} = {\rm{ }}9\mu J\)
Hướng dẫn giải:
- Sử dụng định luật ohm: I = E /(R + r)
- Năng lượng của mạch dao động: \(W = \frac{1}{2}L{i^2} + \frac{1}{2}C{u^2}\)
