Câu hỏi:
2 năm trước
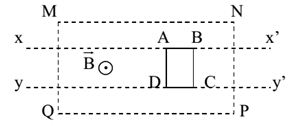
Một mạch kín hình vuông, cạnh 10cm, đặt vuông góc với một từ trường đều có độ lớn thay đổi theo thời gian. Tính tốc độ biến thiên của từ trường, biết cường độ dòng điện cảm ứng i = 2A và điện trở của mạch r = 5Ω.
Trả lời bởi giáo viên
Đáp án đúng: a
Theo định luật Ôm ta có: \(\left| i \right| = \dfrac{{\left| {{e_c}} \right|}}{r}\)
→ Độ lớn của suất điện động cảm ứng là: \(\left| {{e_c}} \right| = \left| i \right|.r = 2.5 = 10V\)
Mặt khác: \(\left| {{e_c}} \right| = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = \left| {\dfrac{{\Delta B.S}}{{\Delta t}}} \right| = \left| {\dfrac{{\Delta B}}{{\Delta t}}} \right|.S \Rightarrow \left| {\dfrac{{\Delta B}}{{\Delta t}}} \right| = \dfrac{{\left| {{e_c}} \right|}}{S}\)
Mạch kín là hình vuông \( \Rightarrow S = {a^2} = {\left( {{{10.10}^{ - 2}}} \right)^2} = 0,01{m^2}\)
→ Tốc độ biến thiên của từ trường là: \(\left| {\dfrac{{\Delta B}}{{\Delta t}}} \right| = \dfrac{{\left| {{e_c}} \right|}}{S} = \dfrac{{10}}{{0,01}} = 1000\,\left( {T/s} \right)\)
Hướng dẫn giải:
+ Biểu thức định luật Ôm: \(I = \dfrac{E}{r}\)
+ Độ lớn của suất điện động cảm ứng: \(\left| {{e_c}} \right| = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right|\)
+ Từ thông: \(\Phi = BS.\cos \alpha ;\,\,\alpha = \left( {\overrightarrow n ;\overrightarrow B } \right)\)
+ Tốc độ biến thiên của cảm ứng từ: \(\dfrac{{\Delta B}}{{\Delta t}}\)
Câu hỏi khác
- Đề kiểm tra 15 phút chương 5: cảm ứng điện từ - đề số 4 Lý 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 5: cảm ứng điện từ - đề số 4 Lý 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 5: cảm ứng điện từ - đề số 2 Lý 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 5: cảm ứng điện từ - đề số 2 Lý 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 5: cảm ứng điện từ - đề số 3 Lý 11 có lời giải chi tiết
