Câu hỏi:
2 năm trước
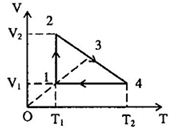
Một lượng khí biến đổi theo chu trình biểu diễn bởi đồ thị. Cho biết \({p_1} = {p_3}\), \({V_1} = 1{m^3}\), \({V_2} = 4{m^3}\), \({T_1} = 100K,{T_4} = 300K\). \({V_3} = ?\)
Trả lời bởi giáo viên
Đáp án đúng: d
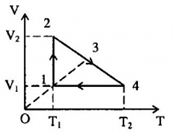
- Quá trình \(\left( 1 \right) \to \left( 2 \right)\): đẳng nhiệt \({T_2} = {T_1} = 100K,{V_2} = 4{m^3}\)
- Quá trình \(\left( 4 \right) \to \left( 1 \right)\): đẳng tích \({V_4} = {V_1} = 1{m^3};{T_4} = 300K\)
- Quá trình \(\left( 2 \right) \to \left( 4 \right)\): \(V = aT + b\)
+ Trạng thái \(\left( 2 \right)\): \(4 = 100{\rm{a}} + b\) (1')
+ Trạng thái \(\left( 4 \right)\): \(1 = 300{\rm{a}} + b\) (2')
Từ \(\left( 1' \right)\) và \(\left( 2' \right)\) suy ra: \(\left\{ \begin{array}{l}a = - \frac{3}{{200}} = - 1,5\\b = 5,5\end{array} \right.\)
Ta suy ra: \(V = - \frac{3}{{200}}T + 5,5\)
- Quá trình \(\left( 1 \right) \to \left( 3 \right)\): đẳng áp \(V = \frac{{{V_1}}}{{{T_1}}}T = \frac{1}{{100}}T{\rm{ }}\left( 4 \right)\)
Vì \(\left( 3 \right)\) là giao điểm của hai đường \(\left( 2 \right) - \left( 4 \right)\) và \(\left( 1 \right) - \left( 3 \right)\) nên:
\(\begin{array}{l} - \frac{3}{{200}}{T_3} + 5,5 = \frac{1}{{100}}{T_3}\\ \to {T_3} = 220K\end{array}\)
Ta suy ra: \({V_3} = \frac{1}{{100}}.220 = 2,2{m^3}\)
Hướng dẫn giải:
Đọc đồ thị V-T
Xác định các quá trình
