Một lò xo có độ cứng \(k\), có chiều dài tự nhiên \({l_0}\) một đầu giữ cố định ở A đầu kia gắn vào quả cầu khối lượng \(m\) có thể trượt không ma sát trên mặt bàn nằm ngang. Thanh \(\left( \Delta \right)\) quay đều với tốc độ góc \(\omega \) quanh trục \(\left( \Delta \right)\) thẳng đứng. Tính độ dãn của lò xo khi :
\({l_0} = 25cm,\omega = 20\pi \left( {rad/s} \right),m = 5g;k = 100N/m.\) Lấy \({\pi ^2} = 10\).
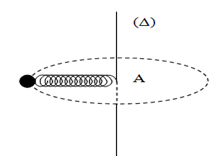
Trả lời bởi giáo viên
Các lực tác dụng vào vật :
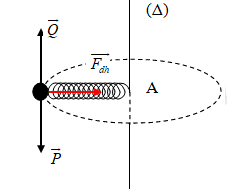
+ Quả cầu chuyển động tròn đều với tốc độ góc \(\omega \) quanh trục \(\left( \Delta \right)\)
+ Lực đàn hồi lúc này đóng vai trò là lực hướng tâm.
\( \Rightarrow {F_{dh}} = {F_{ht}} \Leftrightarrow k.\Delta l = m{\omega ^2}R\)
Trong đó :
+ \(\Delta l\) là độ dãn của lò xo ;
+ R là bán kính quỹ đạo \( \Rightarrow R = l = {l_0} + \Delta l\)
Theo bài ra ta có : \(\left\{ \begin{array}{l}k = 100N/m\\m = 0,005kg\\R = 0,25 + \Delta l\\\omega = 20\pi \,\,\left( {rad/s} \right)\end{array} \right.\)
\(\begin{array}{l} \Rightarrow 100.\Delta l = 0,005.{\left( {20\pi } \right)^2}.\left( {0,25 + \Delta l} \right)\\ \Leftrightarrow 100.\Delta l = 20.\left( {0,25 + \Delta l} \right) \Leftrightarrow 100.\Delta l = 5 + 20.\Delta l\\ \Leftrightarrow 80.\Delta l = 5 \Rightarrow \Delta l = 0,0625m = 6,25cm\end{array}\)
Hướng dẫn giải:
+ Hợp lực của các lực tác dụng lên vật đóng vai trò là lực hướng tâm.
+ Công thức tính độ lớn lực hướng tâm: \({F_{ht}} = \dfrac{{m{v^2}}}{r} = m.{\omega ^2}r\)
+ Lực đàn hồi: \({F_{dh}} = k.\Delta l\)